|
PRACTICE MULTIPLYING AND DIVIDING FRACTIONS |
|
NetScape 3.0+ or I.E. 4.0+ needed
|
Suggestions for this self exam: |
|
[A] |
Study text section 4.2 , but then keep your book closed during this
entire test |
|
[B] |
Enter your answers in the boxes provided. Check them when you've finished. |
|
[C] |
|
Remember the general rules: |
a
b |
. |
c
d |
= |
ac
bd |
and also |
a
b |
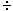 |
c
d |
= |
ad
bc |
|
| [1] |
In the answer boxes, enter the correct reduced product: |
|
| [2] |
In the answer boxes, enter the correct reduced product: |
|
| [3] |
In the answer boxes, enter the correct reduced quotient: |
|
| [4] |
In the answer boxes, enter the correct reduced quotient: |
|
| [5] |
In the answer boxes, enter the correct reduced product: |
|
| [6] |
In the answer boxes, enter the correct reduced product: |
|
| [7] |
In the answer boxes, enter the correct reduced quotient: |
|
| [8] |
In the answer boxes, enter the correct reduced quotient: |
|
| [9] |
In the answer boxes, write as one simple reduced fraction.
A "simple fraction" is a fraction whose numerator and denominator
do not contain other fractions; the original fraction
below is not a simple fraction: |
| |
|
| [10] |
In the answer boxes, write as one simple reduced fraction.
A "simple fraction" is a fraction whose numerator and denominator
do not contain other fractions; the original fraction
below is not a simple fraction: |
| |
|
| [11] |
In the answer boxes, write as one simple reduced fraction.
A "simple fraction" is a fraction whose numerator and denominator
do not contain other fractions; the original fraction
below is not a simple fraction: |
| |
|
|
|
 |
This page last updated
31 May 2001 |
|