Thus, x - 1 must lie between -3 and +3, that is:
Both -3 < x - 1 and x - 1 < +3
Add +1 to all sides, to get:
Both -3 + 1 < x - 1 + 1 and x - 1 + 1 < +3 + 1
Both -2 < x and x < +4
| In other words: -2 < x < 4 |
Solution set of |x - 1| < 3 pictured on a number line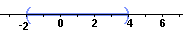 Solution set of |x - 3| > 2 [from #6 above] 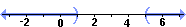 Thus the FINAL SOLUTION to #8 is the overlap (or intersection) of the above two solutions: 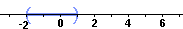 |
| Final Solution Set in interval notation: ( - 2, 1 ) |