WORDS WITH LOGICAL CONTENT IN PROBABILITY PROBLEMS
- The union of two sets, A and B, written A
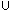 B,
is the set of all objects which are either a member of the the set A
or a member of the set B. B,
is the set of all objects which are either a member of the the set A
or a member of the set B.
- The intersection of two sets, A and B, written A
 B,
is the set of all objects which are both a member of the the set A
and a member of the set B. B,
is the set of all objects which are both a member of the the set A
and a member of the set B.
- The complement of a set A, written A',
is the set of all objects which are not a member of the the set A.
- (Conditional probability) The probability of the event A, given that the event
B has occured, written P(A | B), is equal to P(A
 B)
divided by P(B) B)
divided by P(B)
|
The RED WORDS (also underlined) above have logical content, revealing the stucture of a set, or its relationship to another set.
These RED WORDS have many synonyms in English, and the words are not always used with logical content.
Thus, in [2] above, the word "and" occurs twice; the first "and" has little logical content, merely noting two sets; the second "and"
has logical content, linking two properties (or qualities) of points in A  B.
B.
EXAMPLES OF LOGICAL CONTENT IN PROBLEMS
Red words (also underlined) have logical content.
[11]
Two people are selected randomly from a group of 12 Republicans and 10 Democrats.
[a] Find the probability that both are Democrats. (See [2] above)
[b] Find the probability the one is a Republican and
one is a Democrat. (See [2] above)
[c] Find the probability that neither is a Republican. (See [3] above)
|
[12]
Two good bulbs and seven bad bulbs are mixed in a box. Two bulbs are withdrawn.
[a] Find the probability that at least one bulb is good. (See [1] above)
[b] Find the probability the one bulb is good and
the other is not. (See [2] above)
[c] Find the probability that neither is a bad bulb. (See [3] above)
|
Note that the word "not" above is not used logically, but is used only to identify a bulb type. This "not" could be replaced with "bad".
[13]
Three people are selected from a group of seven men and 5 women.
[a] Find the probability that the first two are women and the third is a man. (See [2] above)
[b] Find the probability that the first two are women if the third is a man. (See [4] above)
[c] Find the probability that the first two are women given the third is a man. (Same as [b] above)
|
[14]
Soft drinks in a cooler are 55% Pepsi and 45% coke. 40% of the Pepsi are diet, and
30% of the coke are diet. A drink is randomly selected and
found to be a diet drink.. (See [4] above for all red underlined words)
[a] Find the probability that the drink is a Pepsi.
[b] Find the probability that the drink is a not a Pepsi. (See [3] above)
|
Note that the entire red underlined sentence above could have been re-written as
"GIVEN THAT a randomly selected drink was found to be a diet drink.",
which makes this look more like [4] above.
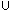 B,
is the set of all objects which are either a member of the the set A
or a member of the set B.
B,
is the set of all objects which are either a member of the the set A
or a member of the set B.
 B,
is the set of all objects which are both a member of the the set A
and a member of the set B.
B,
is the set of all objects which are both a member of the the set A
and a member of the set B.
 B)
divided by P(B)
B)
divided by P(B)

