Mathematics 760-143
Final Exam |
|
Do not write on this test until
you enter Prof McFarland's office |
|
________________________
PRINT name above AFTER
entering Prof's office |
Answer each question by placing the proper LETTER in the blank at the left
|
_____[1] |
The number of subsets of a set with 10 elements is: |
|
(a) 10 |
(b) 100 |
(c) 1024 |
(d) 2048 |
(e) 512 |
|
|
_____[2] |
Last Monday, the county jail had 200 prisoners. Of these, 130 were
accused of felonies, and 121 were accused of misdemeanors. How
many prisoners were accused of both a felony and a misdemeanor? |
|
(a) 11 |
(b) 51 |
(c) 70 |
(d) 79 |
(e) 71 |
|
|
_____[3] |
The slope of the line
3y - 2x - 4 = 0
is: |
|
|
_____[4] |
In a class of 15 people, exactly 3 got an A. If 2 people
are randomly chosen from this class, what is the probability
that at least one of these 2 got an A ? |
|
|
_____[5] |
A box contains 3 defective lights and 5 non-defective lights.
The lights are tested
one at a time without replacement. What is the probability that
the 3 defective bulbs will be found in the first 3 tests? |
|
|
_____[6] |
The inverse of the matrix |
|
is: |
|
_____[7] |
The solution set for the system |
|
is best described as follows: |
|
| |
(a) undefined |
|
(c) { (x,y) | y = (-2/3)x + (5/3) } |
(d) inconsistent |
(e) set of all points |
|
|
_____[8] The number of slack variables needed to solve the problem at the right is : |
| |
(a) 1 |
(b) 2 |
(c) 3 |
(d) 4 |
(e) 0 |
|
Maximize P = 10x + 12y
subject to:
4x + 2y  20 20
5x + 4y  50 50
2x + 3y  25 25
x 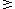 0 ; y 0 ; y 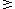 0 0 |
|
|
_____[9] |
A medical test detects H.I.V. Among those who
have H.I.V., the test will detect the disease with probability
0.95; among those who do NOT have H.I.V., the test will falsely
claim that H.I.V. is present with probability 0.0125. Among
those who take this test, 4% have H.I.V.
The test is given to Lucille Jones, and indicates that she has
H.I.V. What is the probability that Lucille actually has H.I.V.? |
|
(a) 0.04 |
|
|
(d) 0.125 |
(e) 0.76 |
|
|
_____[10] |
The probability that both Barb and Bob are both on the same committee
of 4 which is chosen from their class of 10 people is: |
|
Bring this exam, UNMARKED, to McCutchan Hall 317 anytime during the following times:
noon  10 PM Monday 9 May 2016
10 PM Monday 9 May 2016
9 AM  2 PM Tuesday 10 May 2016
2 PM Tuesday 10 May 2016
If you have not already filled out a class evaluation, you will be invited to do so when you arrive.