[1]

(a)(1 pt) Enter the number of events in the sample space {a, b, c} (b)(2 pts) The Venn diagram at the right contains 8 pieces or segments, each with a checkbox. Click those boxes which are located in pieces of the set A (B C)' (c)(2 pts) Enter an integer (such as 24 or 2234) equal to C(13,5) ; C(13,5) = .

[2]	A survey of magazine preferences of 100 students revealed that : 40 read Time 12 read Time and US News 30 read Newsweek 10 read Newsweek and US News 25 read US News 4 read all three 15 read Time and Newsweek
	(a)(3 pts) Place numbers in the appropriate parts of the Venn diagram at the right so as to interpret the given information. Scoring: 1 point for center number only 2 points for center number and 3 adjacent numbers only.
	(b)(1 pt) How many students read at least one magazine?
	(c)(1 pt) How many students read exactly two magazines?

In the above Venn diagram : T = set of students who read Time N = set of students who read Newsweek U = set of students who read US News

[3]	(a)(1 pt) In the maze at the right, a rat (start) passes through 3 one-way doors left-to-right to the finish. Two paths are the same if they use the same doors. How many different paths are there?	start finish
	(b)(2 pts) Four balls are chosen from an urn containing 8 white balls and 7 blue balls. In how many ways can exactly 3 of the 4 balls be blue?
	(c)(2 pts) How many different 5-card poker hands are there?

[4]	(a)(2 pts)(a) In how many ways can a TV manager schedule all 6 different commercials into 6 available time slots reserved for commercials?
	(b)(2 pts) Let E, F, and G be events in a sample space S. Check the alternative (at the right) which is the symbolic name of : "The event that none of the events E, F, or G occurs." On a paper test, the student would write the answer rather than choose from a list of alternatives. E' F' G' E' F' G' (E F G)' (E' F' G' )'
	(c)(1 pt) One card is drawn from a standard 52-card deck ; what is the probability that the card is a diamond?

[5]	(a)(2 pts) A pair of dice is cast ; what is the probability that one die shows "6" and the other shows less than 3?
	(b)(1 pt) A pair of fair dice is cast ; what is the probability that the faces show the same number?
	(c)(2 pts) Let E and F be two mutually exclusive events, for which P(E) = 0.2 and P(F) = 0.5 ; find P(EF).

[6]	(a)(2 pts) Four balls are drawn from an urn containing 30 white balls and 50 blue balls; what is the probability that all of the balls are blue?
	(b)(1 pt) In a lottery, a 4-digit number is picked (such as 0226); what is the probability that a lottery player gets at least the first digit correct?
	(c)(2 pts) A druggist must randomly choose 4 brands from amongst six brands A,B,C,D,E, and F to stock in her store. What is the probability that one of the brands will be B?

[7]	(a)(2 pts) Using data from the tree diagram at the right, find P(E).
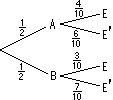	(b)(2 pts) Again using data from the tree diagram at the right, find P(AE).
	(c)(1 pt) Click whichever of the boxed statements below is true: A and E are independent A and E are not independent

[8]	An experiment uses 3 coins: a penny with 2 heads, a nickel with a head and a tail but P(heads) = ¾ , and a quarter with P(heads) = P(tails) = ½. A coin is chosen at random, is flipped, and the result came up heads. What is the probability that the chosen coin was the penny?
	(a)(2 pts) Choose one of 6 definitions of D (brown box below) and choose one of the 5 clusters of definitions for A , B , and C (olive box below) which are needed to the answer to the underlined question (above) using Bayes Formula? Your choices should make P(A | D) equal to the answer to that underlined question. Recall Bayes Formula (not given on paper tests): P(A|D) = P(A)P(D|A) P(A)P(D|A) + P(B)P(D|B) + P(C)P(D|C)
Let D = probability that the coin came up heads Let D = event that the coin came up heads Let D = event that a coin was flipped Let D = event that the penny came up heads Let D = event that the nickel came up heads Let D = probability that the penny came up heads Let D = probability that the nickel came up heads Let D = probability that the quarter came up heads
Let A = event that the chosen coin was a penny Let B = event that the chosen coin was a nickel Let C = event that the chosen coin was a quarter Let A = event that the penny came up heads Let B = event that the nickel came up heads Let C = event that the quarter came up heads Let A = event that the chosen coin was a penny given that it came up heads Let B = event that the chosen coin was a nickel given that it came up heads Let C = event that the chosen coin was a quarter given that it came up heads   Let A = probability that the chosen coin a the penny given that it came up heads Let B = probability that the chosen coin a the nickel given that it came up heads Let C = probability that the chosen coin a the quarter given that it came up heads Let A = event that the chosen coin came up heads given that it was the penny Let B = event that the chosen coin came up heads given that it was the nickel Let C = event that the chosen coin came up heads given that it was the quarter
	(b)(1 pt) Check the alternative below which correctly interprets the number " ¾ " in problem [8] above. A correct answer (and 1 point) here requires a correct answer to [8a] above,
P(B) P(BD) P(BD) P(B | D) P(D | B) P(B)P(D) P(B)P(D) P(D)P(B) P(B) P(D)
	(c)(1 pt) Check the alternative below which correctly interprets the number "½" in problem [8] above. A correct answer (and 1 point) here requires a correct answer to [8a] above,
P(C) P(CD) P(CD) P(C | D) P(D | C) P(C)P(D) P(C)P(D) P(D)P(C) P(C) P(D)
	(d)(1 pt) Find P(A | D), that is, find the probability that the chosen coin was the penny.