The above information is from your computer : be sure it is correct.
Best submitted over the internet by 3:00 PM on Wednesday 26 September 2018

Math 76O-250 Calculus for Business
Self-marking on-line assignment 4
Finding Critical Values and Candidates for (mostly) Polynomial Functions
Best submitted over the internet by 3:00 PM on Wednesday 26 September 2018

Methods will be discussed in class

Click or type the appropriate answer for each question.
When you are sure of your answers, send them to your Professor:

Enter your name above
Enter preferred email address;
include @ and whatever follows
Enter student I.D.


Using a calculator is NOT allowed on this practice assignment.
The exercises below ask you to find critical values and candidates, but not to test them.

The term CRITICAL VALUE (of a function f(x) ) describes a value of x for which f '(x) = 0 or is undefined. Some texts use an alternate term "critical number or critical point".

The term CANDIDATE describes a value of x for which f "(x) = 0 or is undefined. Some texts use the phrase " second order critical value".

In an interactive tutorial elsewhere on this website, you can see several graphical examples of CRITICAL VALUES and CANDIDATES.

Important tools in locating CRITICAL VALUES and CANDIDATES are those used to factor polynomials in a typical high school algebra course.

Here is a solution of a more challenging problem, similar to problems [5] and [8] below, using factoring by grouping.

If f (x) = x4 + 8x3 - 8x2 - 96x + 3 ,
Then f '(x) = 4x3 + 24x2 - 16x - 96 ,
factor out a common factor of 4
then f '(x) = 4 [ x3 + 6x2 - 4x - 24 ] ,
now group terms, preparing to factor the groups, just as in high school
then f '(x) = 4 [ (x3 + 6x2 ) - ( 4x + 24) ] ,
now factor each group
then f '(x) = 4 [ x2 ( x + 6 ) - 4 (x + 6) ] ,
the groups have a common factor of ( x + 6 ) : factor it out
then f '(x) = 4 ( x + 6 ) ( x2 - 4) ,
finally, factor ( x2 - 4)
then f '(x) = 4 ( x + 6 ) ( x + 2) ( x - 2) ,
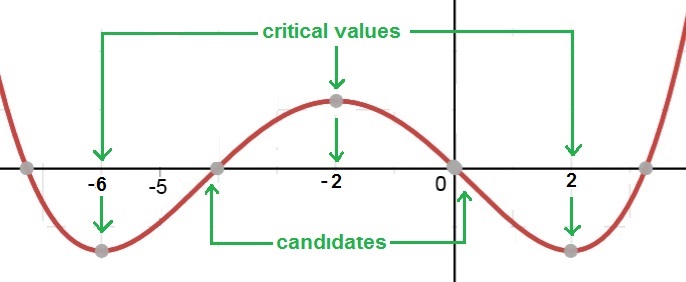
Critical values will be values of x which make the above expression equal to 0

The smallest critical value of f (x) is therefore -6
The middle critical value of f (x) is therefore -2
The largest critical value of f (x) is therefore 2
To find the 2 candidates for this function, differentiate again: a bit messy but similar to above:
thus f "(x) = 12x2 + 48x - 16 : Candidates are values of x for which 12x2 + 48x - 16 = 0
This polynomial does not have "nice" factors, so use the Quadratic Formula
If ax2 + bx + c = 0, then   x =  
- b ±

 b2 - 4ac
2a
Original Equation: 12x2 + 48x - 16 = 0
Identify values of "a", "b", and "c": a = 12, b = 48, c = - 16
Substitute these values into the quadratic formula, to get:
x =  
-48 ±  

 (48)2 - 4(12)(-16)
2(12)
  =  
-48 ±  

  3024
24
  ≈  
- 4.291
+0.291
The candidates for the original function are therefore approximately (- 4.291) and 0.291

[1] (value 10%) If f (x) = 2x2 + 8x + 3 ,
then the one critical value of f is (enter a number)

[2] (value 10%) If f (x) = x3 - 6x2 + 12x + 6 ,
then the one critical value of f is (enter a number)

[3] (value 10%) If f (x) = x3 + 3x2 - 9x + 12 ,
then the SMALLER critical value of f is (enter a number)
and the LARGER critical value of f is (enter a number)

[4] (value 10%) If f (x) = ( x2 - 4 )10 ,
then the SMALLEST critical value of f is (enter a number)
and the MIDDLE critical value of f is (enter a number)
and the LARGEST critical value of f is (enter a number)

[5] (value 10%) If f (x) = x4 - 4x3 - 8x2 + 48x + 4 , (see a similar example above)
then the SMALLEST critical value of f is (enter a number)
and the MIDDLE critical value of f is (enter a number)
and the LARGEST critical value of f is (enter a number)

[6] (value 10%)
If f (x) =

 x + 1
then the one critical value of f is (enter a number)

[7] (value 10%) If f (x) = x3 - 12x2 + 18x + 30 ,
then the one candidate of f is (enter a number)

[8] (value 10%) If f (x) = x4 - 2x3 - 12x2 + 12x + 24 ,
then the SMALLER candidate of f is (enter a number)
and the LARGER candidate of f is (enter a number)

[9] (value 10%)
If f (x) = x2

x2 + 3
then the SMALLER candidate of f is (enter a number)
and the LARGER candidate of f is (enter a number)

[10] (value 10%)
If f (x) =

 x + 1
then the one candidate of f is (enter a number)

Roughly how many minutes did you spend working on this quiz :

Comments or complaints regarding this on-line assignment

Press the "display scoring" button to check your score before submitting :
When you have done your best above, submit your results to Professor HERE (below).
Be sure your email address is correct above: your graded assignment will be immediately returned there!

Re-load page for new fortune