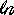 x (for x > 0),
x (for x > 0),|
The above information is from your computer : be sure it is correct. Best submitted over the internet by 3:00 PM on Wednesday 17 October 2018 |
Math 76O-250 Calculus for Business
Self-marking on-line assignment 7
Finding Critical Values and Candidates for Exponential and Logarithmic Functions
Best submitted over the internet by 3:00 PM on Wednesday 17 October 2018
Methods will be discussed in class
| [1] (value 10%) | If f (x) = (x + 1) ex , |
| then the one critical value of f is (enter a number) |
| [2] (value 10%) | If f (x) = (x - 1) e - x , |
| then the one critical value of f is (enter a number) |
| [3] (value 10%) | If f (x) = x2 ex , | |
|
| [4] (value 10%) | If f (x) = x2 e -x² , | ||
|
| [5] (value 10%) |
If f (x) = x2 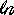 x (for x > 0), x (for x > 0), |
| then the one critical value of f is (enter a decimal accurate to 0.01: answer is between 0 and 1) |
| [6] (value 10%) | (see problem [1] above) If f (x) = (x + 1) ex , |
| then the one candidate of f is (enter a number) |
| [7] (value 10%) | (see problem [2] above) If f (x) = (x - 1) e - x , |
| then the one candidate of f is (enter a number) |
| [8] (value 10%) | (see problem [3] above) If f (x) = x2 ex , | |
|
| [9] (value 10%) | If f (x) = ex - e - x , |
| then the one candidate of f is (enter a number) |
| [10] (value 10%) |
(see problem 5) If f (x) = x2 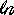 x (for x > 0), x (for x > 0), |
| then the one candidate of f is (enter a decimal accurate to 0.01: answer is netween 0 and 1) |
Roughly how many minutes did you spend working on this quiz :
Comments or complaints regarding this on-line assignment
|
Press the "display scoring" button to check your score before submitting : |
|
|
When you have done your best above, submit your results to Professor HERE (below). Be sure your email address is correct above: your graded assignment will be immediately returned there! |
|
 |
 |