|
|
A DIFFERENTIAL EQUATION (D.E.) is an equation which "contains"
derivatives of some function. |
|
EXAMPLES : |
[a] y' = 2
[b] y' = 3x2 - 4
[c] y' = y2
[d] y' = y'
[e] (y' )2 + y2 = 1 |
|
Note that the word "contains" is not
clearly defined, so that in the 4th DE,
y' = y',
is y' really present?? |
|
|
|
A function y(x) [or just y] is a
PARTICULAR SOLUTION
of a D.E. if the D.E. is a true statement about y. |
| |
As examples, y = 2x is a particular solution of example [a] above,
y = x3 - 4x -1 is a particular solution of example [b] above,
and any function with a derivative is a particular solution of exampe [d] above. |
|
|
The
GENERAL SOLUTION of a D.E. is the set of all
of it's particular soltions, often expressed using a constant C
(or K) which could have any fixed value. |
| |
As examples, y = 2x +C is the general solution of example [a] above,
and y = x3 - 4x + C is the general solution of example [b] above. |
| |
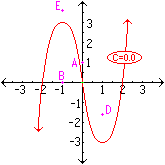
If (as in [b] above), y' = 3x2 - 4
and [y = -4] when [x = 1], then first anti-differentiate [b]
to obtain a GENERAL SOLUTION : y = x3 - 4x + C [as shown in the right figure below].
Then substitute x = 1 and y = -4, to get : -4 = 13 - 4(1) + C.
Solve for C to get C = -1.
Therefore, the PARTICULAR SOLUTION
for which [y = -4] and [x = 1] is [y = x3 - 4x - 1]
Use the graph below to display this particular solution, which
must pass through the point (1, -4). |
| |
| The collection of graphs of all particular solutions of a D.E. completely
fill up space, and no two graphs overlap, much as the layers of a dagwood sandwich. The red graphs in the
right image are playing the same role as the ham, cheese, and lettuce in Dagwood's sandwich in the left image. |
|
|
|
|
The general solution to [b] (named above) is obtained by anti-differentiating
both sides of [b]. If you let your mouse wander across the graph below, you
will see many of the particular solutions of [b], each having the equation
y = x3 - 4x + C, and each labeled with it's own value of "C".
Separable differential equations can
be written in the form
f(y) y' = g(x) : y' = g(x) :
doing this may tax your algebra skills.
An example is at the right :
|
|
Solve the differential equation y' = |
y2

x+1 |
|
|
Solution : first move all y to the left, and all x to the right |
y'

y2 |
= |
1

x+1 |
|
|
Next : Anti-differentiate both sides |
|
|
|
Next : Remove a factor of y' to change variable to y : |
|
|
|
Finally : antidifferentiate (review methods ?): |
-1 y-1 =  (x+1) + C (x+1) + C |
|
or |
y = [-  (x+1) + C] -1 (x+1) + C] -1 |
|
|
|
|
|
Your mouse arrow
can control which particular solution of
y' = 3x2 - 4,
is visible. To keep a chosen solution visible while answering a
question below, slide the mouse arrow off either left or
right edge of the graph. |
|
|
|
 y' = g(x) :
y' = g(x) :










 (x+1) + C
(x+1) + C (x+1) + C] -1
(x+1) + C] -1