| Algebra Skills test answers |  |
| Algebra Skills test answers |  |
[1] State the degree of the polynomial: x3 - x2 + x4
[2] Remove parentheses and combine like terms: -4m2 + 3n2 - 5n - [3m2 - 5n2 + 2n - (3m2 - 4n2)]
= -4m2 + 3n2 - 5n + 5n2 - 2n - 4n2 = -4m2 + 4n2 - 7n
[3] Factor out the largest common factor: 9x2y2z4 - 18x3y2z
[4] Factor out the largest common factor, and then combine like terms: 4(3-x)2 - (3-x)3 + 3(3-x)
[5] Factor: 27x3 - 64y3
[6] Factor, i.e., write as A times B for some A & B: (m-p)2 + 4(m-p) + 4
[7] Simplify by writing as one term (it is 3 terms, now): 3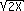 -
- 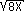 -
- 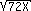
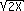 - 2
- 2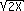 - 6
- 6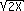 = -5
= -5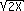
[8] Solve for x: 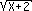 -
- 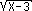 = 1 : square both sides to get
= 1 : square both sides to get
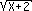 )2 - 2
)2 - 2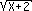 .
.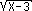 + (
+ (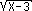 )2 = 12
)2 = 12
(x + 2) - 2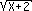 .
.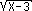 + (x - 3) = 1
+ (x - 3) = 1
2x - 2 = 2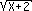 .
.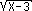
x - 1 = 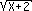 .
.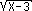 : now square both sides again to get
: now square both sides again to get
x2 - 2x + 1 = (x + 2)(x - 3) = x2 -x - 6 : the red terms cancel
-2x + 1 = -x - 6
x = 7
[9] Find all values of x for which 10x2 + x - 21 = 0
Two possible methods:
| [A] Use quadratic formula with a=10, b=1, and c=-21, to get x = |
|
[10] Solve for x: log(4x) = log(2) + log(x-3): combine right side as
A couple of students correctly noticed that x = -3 will make numbers in the original equation into complex numbers, and in some algebra courses, such situations are interpreted as if there were no solution (actually, no "real" solution)
 |
 |
 |
|