| an = |
|
= [ f (n)(0) ] ÷ n ! |
A Power series is a series (or formal sum) with the form : a0 + a1x1 + a2x2 + a3x3 + a4x4 + a5x5 + ....
A Taylor series about the base number 0 for a function f is a Power series in which the numbers " an " are chosen as follows:
| an = |
|
= [ f (n)(0) ] ÷ n ! |
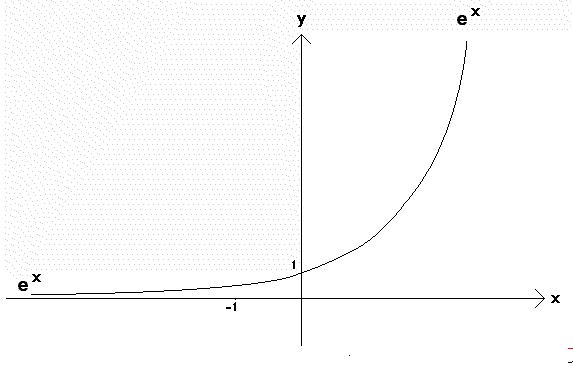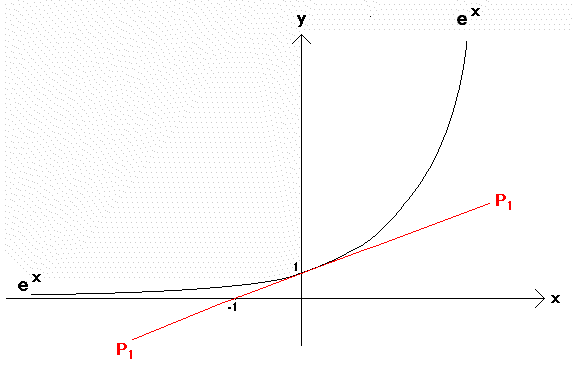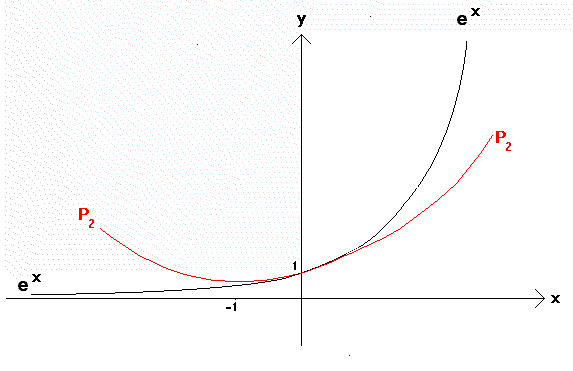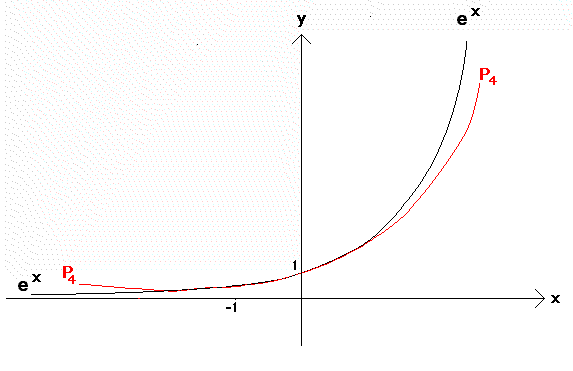
The first 5 Taylor Polynomials (in red) for y = ex (in black) at base a = 0
For each value of x, Taylor polynomials become successively better approximations to ex as more terms are added.
Each Taylor Poynomial becomes a gradually poorer approximation to ex as x moves away from the base point a = 0
P0
= 1
 |
Here we create several terms of the Taylor series (about the base a=0 ) for f(x) = 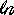 (1 - x) (1 - x)Note: x must be less than 1 because ( 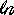 x ) is not defined for negative x x ) is not defined for negative x |
||||||||||||
| ||||||||||||
|
| n | function: f (n)(x) |
value at
x = 0 |
an |
| 0 |
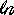 (1 - x) (1 - x) |
||
| 1 | (- 1) (1 - x)- 1 | ||
| 2 | (- 1) (1 - x)- 2 | ||
| 3 | (- 1)(2) (1 - x)- 3 | ||
| 4 | (- 1)(2)(3) (1 - x)- 4 | ||
| 5 | (- 1)(2)(3)(4) (1 - x)- 5 |
|
| n | function: f (n)(x) | f (n)(0) | an |
| 0 |
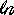 (1 - x) (1 - x) |
0 | |
| 1 | (- 1) (1 - x)- 1 | - 1 | |
| 2 | (- 1) (1 - x)- 2 | - 1 | |
| 3 | (- 1)(2) (1 - x)- 3 | (- 1)(2) | |
| 4 | (- 1)(2)(3) (1 - x)- 4 | (- 1)(2)(3) | |
| 5 | (- 1)(2)(3)(4) (1 - x)- 5 | (- 1)(2)(3)(4) |
|
| n | function: f (n)(x) | f (n)(0) | an = [ f (n)(0) ] ÷ n ! |
| 0 |
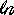 (1 - x) (1 - x) |
0 | 0 ÷ 0! = 0 ÷ 1 = 0 |
| 1 | (- 1) (1 - x)- 1 | - 1 | (- 1) ÷ 1! = (- 1) ÷ 1 = (- 1) |
| 2 | (- 1) (1 - x)- 2 | - 1 | (- 1) ÷ 2! = (- 1) ÷ 2 = (- ½) |
| 3 | (- 1)(2) (1 - x)- 3 | (- 1)(2) | (- 1)(2) ÷ 3! = (- 1)(2) ÷ (3)(2) = (- ⅓) |
| 4 | (- 1)(2)(3) (1 - x)- 4 | (- 1)(2)(3) | (- 1)(2)(3) ÷ 4! = (- 1)(2)(3) ÷ (2)(3)(4) = (- ¼) |
| 5 | (- 1)(2)(3)(4) (1 - x)- 5 | (- 1)(2)(3)(4) | (- 1)(2)(3)(4) ÷ 5! = (- 1)(2)(3)(4) ÷ (2)(3)(4)(5) = (- ⅕) |