Bayes Rule

Given Events E₁ and F, write two conditional probabilities :

P(E1 | F) =	P(E1 F) P(F)	or	P(E1 F) =	P(E1 | F)P(F)
P(F | E1) =	P(E1 F) P(E1)	or	P(E1 F) =	P(F | E1)P(E1)
			left sides equal above means right sides equal below

P(E₁ | F)P(F) = P(F | E₁)P(E₁)

Divide both sides of the above by P(F) , to get a SIMPLE FORM OF BAYES RULE :

P(E1 | F) = P(E1)P(F | E1) P(F)

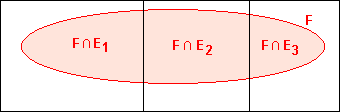
The denominator P(F) above can be re-written if the sample space (and hence F) are partitioned, or divided, into 2 or more non-overlapping pieces, as implied in the classic box-cutting magic trick, and its representation using sets in the figures (right) :
	Don't worry : This won't hurt at all Prefer Josh to Madonna?
	E1   E2   E3

If E₁ , E₂ , and E₃ do not overlap, then (F E₁) , (F E₂) , and (F E₃) also do not overlap, and hence
P(F) = P(F E₁) + P(F E₂) + P(F E₃) ; re-writing each term as a product (as at the top of this page) :

P(F) = P(E₁)P(F | E₁)   +   P(E₂)P(F | E₂)   +   P(E₃)P(F | E₃) ;

We can then re-write the simpler form (above) to a LARGER FORM OF BAYES RULE :

P(E1 | F) = P(E1)P(F | E1) P(E1)P(F | E1) + P(E2)P(F | E2) + P(E3)P(F | E3)

SEE INTERACTIVE EXAMPLE

Ooops

This page last updated 7 October 2013