AN EXAMPLE OF THE LIMIT METHOD
FOR FINDING THE DERIVATIVE OF f
Please review the general discussion before trying this example.
We pick a relatively simple example here : f(x) = x3 .
First recall the definition of "derivative" for any function f :
| f ' (x) = |
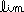 |
h 0 0 |
|
f(x+h) - f(x)
(x+h) - x |
|
Now we interpret the functional notation for our particular function f(x) = x3 ;
at this point, you may want to review the binomial theorem :
|
f ' (x) = |
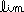 |
h 0 0 |
|
|
Now we must rewrite the fraction, since both top and bottom approach zero :
| = |
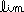 |
h 0 0 |
|
|
[x3 + 3x2h + 3xh2 + h3] - x3 |
          |
| (x+h) - x |
|
Now we cancel two pairs of numbers, colored red above, and factor the top :
At this point, both top and bottom are ZERO if h = 0.
However, if h is NOT ZERO, we cancel the two red h above:
| = |
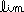 |
h 0 0 |
|
[3x2 + 3xh + h2] |
And now the limit can be readily seen: the last two terms shrink to ZERO while the first term remains fixed.
= 3
x2 + 0 + 0 = 3
x2 .
Thus, f ' (x) = 3x2
 |
|
 |
This page last
updated 13 February 2016 |
|
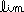
 0
0









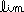
 0
0






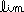
 0
0






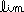
 0
0