(Alternate practice with limits)
A GEOMETRIC VIEW OF THE DERIVATIVE OF A FUNCTION f
|
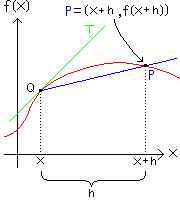
In the figure below, imagine a point Q = (x, f(x)) on the red graph of the function f.
Imagine also a point P which moves along the graph of f, much as a bead moves on a string, with P getting closer and closer to Q.
Imagine the (green) line T tangent to the graph of f at the point Q. Finally, imagine a secant line
through Q and P, shown below in blue.
|
|
( SLOPE OF PQ ) = ( SLOPE OF T ) |
Noticing in the animation above that the horizontal separation between P and Q is h, we can re-write this corrupted language in a more traditional format, as follows:
|
( SLOPE OF PQ ) = ( SLOPE OF T ) |
Then using the definition of the slope of the line PQ, we re-write again:
|
f(x+h) - f(x) (x+h) - x |
= SLOPE OF T |
And finally, we re-write as our DEFINITION OF THE DERIVATIVE OF f:
THE LIMIT METHOD uses the above definition to find f ' (x). In using THE LIMIT METHOD, you may be uncertain how to interpret the symbol f(x+h). It will help to review problem 1 on the functional notation handout. See an example using THE LIMIT METHOD: others will be done in class; the method is a bit cumbersome, but quickly leads to the more familiar "rules for derivatives" such as the power rule. At this point of the year, however, students are expected to avoid the quicker "rules" in finding f ' (x).
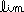
 Q
Q
