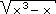FUNCTIONAL NOTATION (problem [1] )
and
COMPOSITE FUNCTIONS (i.e., CHAINS) (problem [2] )
[1] If f(x) = 3x+2 , and if g(x) = x2 - 1, then find the following:
|
a] f(1) |
|
b] f(0) |
|
c] f(-1) |
|
d] f(x+1) |
|
e] f(x-1) |
|
f] f(3x) |
|
|
|
g] f(3x+2) |
|
h] f(-x) |
|
i] f(x2) |
|
j] f(f(x)) |
|
k] f(g(x)) |
|
|
|
|
l] g(1) |
|
m] g(0) |
|
n] g(-1) |
|
o] g(x+1) |
|
p] g(x-1) |
|
q] g(3x) |
|
|
|
r] g(-x) |
|
s] g(x2) |
|
t] g(x2-1) |
|
u] g(f(x)) |
|
v] g(g(x)) |
|
|
| [2]
| The following exercizes practice skills used in THE CHAIN RULE
from Calculus. Composite functions (or chains) have the form y(u(x)). In this situation we may
call u or u(x) the "inner function", and we may call y or y(u)
the "outer function". For the functions h(x) listed below,
choose a u(x) and an y(u), so that their composition
y(u(x)) is equal to the given h(x). |
|
Example: If h(x) = (2x + 1)2, choose u = 2x + 1 and y(u) = u2 |
|
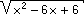
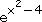
 (3x - 2)
(3x - 2)