Suggestions for this self exam:

[A]	Study the 6 rules for derivatives described in chapter 2. Each of these rules applies to a particular "type" of function, so you must identify the "type" of your function before choosing a rule to differentiate it.

[B]	For each function below, click on the left-most button naming it's type, but DO NOT move the mouse around while you think: that is cheating.

[1] If f(x) = x² + 2x - 5 , then what type is f ?

---

[2] If f(x) = -3(5x³ - 2x + 5) , then what type is f ?

---

[3] If f(x) = 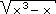, then what type is f ?

---

[4] If f(x) = 5 , then what type is f ?

---

[5] If f(x) =

(1 - 2x)2 (3x - 1)3

, then what type is f ?

---

[6] If f(x) = (2x+1)(3x-2) , then what type is f ?

---

[7] If f(x) = x² , then what type is f ?

---

[8] If f(x) = (x+1)(x-2) - (x+3)(x-5) , then what type is f ?

---

[9] If f(x) =

x + 1 x - 1

, then what type is f ?

---

[10] If f(x) = (1 + x²)⁴ , then what type is f ?

---

[11] If f(x) = (the square root of x) , then what type is f ?

---

[12] If f(x) = 16x² , then what type is f ?

---

[13] If f(x) = 3x^-1 - 2x^-2 + 2x^-3 , then what type is f ?

---

[14] If f(x) =

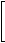(1 - 2x)2 (3x - 1)3

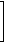3

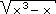, then what type is f ?