|
PRACTICE IDENTIFYING FUNCTION TYPE |
|
(An interactive javascripted self-test)
Suggestions for this self exam:
|
The objective of this page is to give practice choosing the correct rule or tool
to differentiate a function. That is, each derivative rule states the derivative of
a specific function type (such as a "product"), so before differentiating, one must
decide what type of function is being differentiated. Typically, functions are created
much as one puts on clothes, and the differentiation process will act on the
these layers of creation as one removes clothes, the last layer put on becomes
the first layer removed. |
|
[A] |
Refer to the 6 rules for derivatives described in chapter 2. Each
colored icon below names a particular "type" of function. To begin differentiating the function,
you must identify the "type" of your function |
|
[B] |
Keep your mouse arrow to the side as you think. When you have chosen a function
type, test your choice by moving the mouse arrow over the proper button. |
| [1]
If f(x) = x2 + 2x - 5 , then what type of function is f ? (choose one of the 6 types below) |
| [2]
If f(x) = -3(5x3 - 2x + 5) , then what type of function is f ? (choose one of the 6 types below) |
[3]
If f(x) = 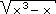 , then what type of function is f ? (choose one of the 6 types below) |
| [4]
If f(x) = 5 , then what type of function is f ? (choose one of the 6 types below) |
| [5]
If f(x) = |
(1 - 2x)2
(3x - 1)3 |
, then what type of function is f ? (choose one of the 6 types below) |
| [6]
If f(x) = (2x+1)(3x-2) , then what type of function is f ? (choose one of the 6 types below) |
| [7]
If f(x) = x2 , then what type of function is f ? (choose one of the 6 types below) |
| [8]
If f(x) = (x+1)(x-2) - (x+3)(x-5) , then what type of function is f ? (choose one of the 6 types below) |
| [9]
If f(x) = |
x + 1
x - 1 |
, then what type of function is f ? (choose one of the 6 types below) |
| [10]
If f(x) = (1 + x2)4 , then what type of function is f ? (choose one of the 6 types below) |
[11]
If f(x) = 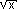 , then what type of function is f ? (choose one of the 6 types below) |
| [12]
If f(x) = 16x2 , then what type of function is f ? (choose one of the 6 types below) |
| [13]
If f(x) = 3x-1 - 2x-2 + 2x-3 , then what type of function is f ? (choose one of the 6 types below) |
| [14]
If f(x) If f(x) = |
 |
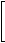(1 - 2x)2
(3x - 1)3 |
 |
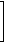3 |
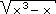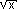, then what type of function is f ? (choose one of the 6 types below) |
