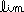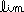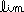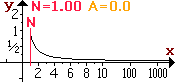|
Recall the FUNDAMENTAL THEOREM OF CALCULUS : |
 |
|
f (x) dx = F(b) - F(a) where F' = f |
|
|
Under the simplest interpretation, " a " , " b " , F(a) , and F(b) must be numbers, and the function
" f " must be defined and continuous in the interval [a,b]. However, we can often extend this tool
to more bizarre situations, such as the following.
A plane region R is called BOUNDED if it is contained
within some circle. Triangles, squares, line segments, and circles are all bounded, but
lines, parabolas, and hyperbolas are unbounded.
An integral is called IMPROPER if it describes the area
of an unbounded region. Thus, the left-hand integral below is "proper" and describes the
area of a triangle. The right-hand integral is improper and describes an area (discussed
in detail below) which extends indefinitely to the right.
|
A "proper" integral : |
|
An "improper" integral : |
 |
|
(2x + 3) dx |
|
|
|
|
One way to study improper integrals is to temporarily chop off an unbounded part
of the area, find the size of the remaining bounded area, and then find the limit as the
chop point is extended to include more and more area. If the limit does not exist, the
area is said to be infinite ; however, often the limit exists, as for the improper
integral above, and that limit becomes the value of the integral.
The chop point in our example will be the red number N .
For the exercises below, moving your mouse across the graph allows you to control the chop number
N and the amount of area counted. If you slide your mouse off
the bottom edge of the graph, the chosen area will remain visible. When you have selected a
chop number N, you may answer the questions below. The shape and scale
of the graph below is exaggerated for artistic effect.
|
Move the mouse arrow
slowly across the graph at the right. THE AMOUNT OF ORANGE AREA WILL CHANGE.
To keep a chosen area visible, slide your mouse off the
bottom edge of the graph. |
|
|
|