Definition 1.

Consider any of these inequalities: A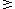B , AB , A > B , A < B. For each such inequality, it's ASSOCIATED EQUATION is A = B. We will abbreviate the phrase "ASSOCIATED EQUATION" to "AE".

Example 2.

The AE for the inequality   "3x - 2y 5"    is    "3x - 2y = 5"  .

Fact 3.

Let A and B be algebraic expressions involving the variables x, y, or others. The graph of the equation A = B divides up space into pieces; within each piece, either [1] ALL points satisfy A > B , or or      [2] ALL points satisfy A < B.

Note 4.

In our situations, A and B will usually involve the two variables "x" and "y", the AE's will have straight-line graphs, and therefore the pieces into which A = B divides space will be "half-planes", that is, the set of points on one side of a straight line.

Note 5.

To graph an inequality (such as A B), first graph it's AE. Then test each piece into which that graph divides space (with "TEST POINTS": red points in figure below). Choose or mark those pieces whose test points satisfy the given inequality (in our example, A B). Thus, in the examples below, the origin ( 0 , 0 ) makes a good test point, for which the stated inequality " x 2 + y 2 1 " is TRUE.

MARKING YOUR GRAPH

ARROWS are used when marking several overlapping regions. Thus, the graph at the right marks the interior of the circle with center (0,0) and radius 1, which solves the inequality " x2 + y2 1 ".
The test points are C = (0,0) and D = (2,0): C satisfies " x2 + y21" since " 02 + 021". On the other hand, D fails to satisfy " x2 + y2 1 ", because " 22 + 02 = 4 > 1 ". Thus, using Fact 3 above, the solution set for our inequality is the set of points on the same side of the circle as is C.

SOLID SHADING is used in the final answers to problems, or where there is only ONE region being shaded. Use the side of your pencil, or in some way completely fill up the visible portion of the space being marked, as at the right.

Practice these ideas with a self-test ?

Definition 6.

The solution set (or graph) of a system of several inequalities is the set intersection of the solution sets of the separate inequalities.

This page last updated 23 June 2007