OPTIMIZING FUNCTIONS
For the graph below, an
up-dated browser is helpful
|
Definition 1 |
A CRITICAL VALUE (CV) of a function f is a number c
for which either: |
| |
| f '(c) = 0 (CV of type (i)) |
| or |
| f '(c) is undefined (CV of type (ii)) |
|
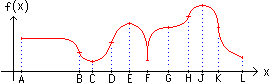
| Note 1: CVs of type ( i ) are at C, E, G, and J below. |
| Note 2: CVs of type ( ii ) are A, F, K, and L below; A and L are domain endpoints. |
| Note 3: At F and K, tangents to the graph of f are VERTICAL, so f ' is undefined. |
Note 4: If x=c is an endpoint in the domain of f (as A and L in figure below),
then we understand that f '(c) is UNDEFINED: a CV of type (ii) above. |
|
|
Definition 2 |
Two numbers are NEARBY if NO CRITICAL VALUE lies between them. |
|
Definition 3 |
A RELATIVE MAXIMUM (REL MAX) of f is a number x=a for which f(a) 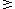 f(x) for all nearby numbers x.
(A, E, and J in figure below). f(x) for all nearby numbers x.
(A, E, and J in figure below). |
| |
|
Definition 4 |
A RELATIVE MINIMUM (REL MIN)
of f is a number x=a for which f(a)  f(x) for all nearby numbers x
(A, C, F, and L in figure below). f(x) for all nearby numbers x
(A, C, F, and L in figure below). |
| |
|
Definition 5 |
A RELATIVE EXTREMUM
of f is a number x=a which is either a relative
maximum or a relative minimum of f. |
| |
|
Definition 6 |
A LEDGE VALUE (LV) of f,
or simply LEDGE, is a number x=a
which is a critical value but NOT a relative extremum. In the
figure below, ledge values occur at G (horizontal ledge)
and K (vertical ledge). |
| |
| |
|
Move the mouse arrow slowly across the graph at the right.
Various features of the graph will be pointed out. |
|
|
 |
|
|
Fact 7: [basic to optimizing] Every relative extremum is a CV. |
|
|
Fact 8: Not all CV's are relative extrema (as G and K above). |
|
|
Definition 9: |
A graph or function is called CONCAVE UP
in an interval if the graph lies ABOVE it's tangents in that interval.
Similarly, this graph is called
CONCAVE DOWN if it lies BELOW it's
tangents. Concavity is illustrated in the
graph shown above |
| |
|
Fact 10a: If
f "(x) > 0 in an interval, then f is concave up there. |
|
(e.g., use a mouse on intervals [B,C] or [C,D] in the figure above) |
|
Fact 10b: If
f "(x) < 0 in an interval, then f is concave down there. |
|
(e.g., use a mouse on intervals [E,F] or [F,G] in the figure above) |
|
Definition 11: |
A CANDIDATE of f
(or 2nd order Critical Value) is a number x = k
at which either f "(k) = 0 or f "(k) is
undefined. It is not always possible to distinguish
candidates by the shape of a graph, but points A, B, D, F, H, K
and L are candidates above. |
| |
|
Definition 12: |
An INFLECTION POINT (IP) is a
candidate at which f "(x) changes sign, and hence
(see Facts 10a/10b) concavity changes.
Points B, D, G, and K above are IPs, as well as candidates. |
| |
OUTLINE OF PROCEDURE FOR OPTIMIZING f(x)
| I. |
Find f '(x) |
| II. |
Find all CV's of f(x) |
| III. |
Test each CV as to what kind of extremum (if any) it is. |
|
There will be 3 tests available, as follows:
| IIIA. Graph test (stated below) |
| IIIB. 1st derivative test (see text Pg.172 and below) |
| IIIC. 2nd derivative test (see text Pg.189 and below) |
|
III A. Graph test for CV: x = c
Calculate f(x) at x = c and at two nearby test values, x = b and x = d,
with b  c c  d: see figure at right. d: see figure at right. |
If BOTH f(c)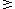 f(b) AND f(c) f(b) AND f(c)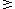 f(d), then c is a relative maximum, f(d), then c is a relative maximum,
as in GRAPH A at the right. |
If BOTH f(c) f(b) AND f(c) f(b) AND f(c) f(d), then c is a relative minimum, f(d), then c is a relative minimum,
as in GRAPH B at the right. |
| Otherwise, c is a ledge (LV), as in GRAPH C at the right |
| |
III B. 1st derivative test for CV: x = c
Calculate f '(x) at 2 nearby test values, x = b and x = d,
with b  c c  d: see figure above. d: see figure above.
|
If f '(b)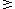 O , and f '(d) O , and f '(d) O , then x = c is a relative maximum; again, see GRAPH A above. O , then x = c is a relative maximum; again, see GRAPH A above. |
If f '(b) O , and f '(d) O , and f '(d)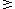 O , then x = c is a relative minimum; again, see GRAPH B above. O , then x = c is a relative minimum; again, see GRAPH B above. |
| Otherwise, x = c is a ledge; again, see GRAPH C above. |
III C. 2nd derivative test for CV of type (i): x = c
|
Calculate f "(x) at x = c. |
| If f "(c) < 0 , then x = c is a relative maximum; again, see GRAPH A above. |
| If f "(c) > 0 , then x = c is a relative minimum; again, see GRAPH B above. |
| If f "(c) = 0 , then x = c could be a max, min, or ledge: use IIIA or IIIB to see which. |
PROCEDURE FOR ANALYZING IPs
(inflection points)
| IV. Find f "(x) |
| V. Find all candidates (see Definition 9 above). |
| VI. Test each candidate k to see
whether or not it is an inflection point, as follows: |
| VIa. |
Calculate f "(b) and f "(d), where b k k d; d;
both b and d must be nearer to k than the next nearest candidate. |
| VIb. |
Only if f "(b) and f "(d) have opposite signs will x = k be
an IP. |
|
|
|
 |
|
 |
This page last updated
12 October 2011 |
|
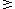 f(x) for all nearby numbers x.
(A, E, and J in figure below).
f(x) for all nearby numbers x.
(A, E, and J in figure below).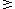 f(x) for all nearby numbers x.
(A, E, and J in figure below).
f(x) for all nearby numbers x.
(A, E, and J in figure below). f(x) for all nearby numbers x
(A, C, F, and L in figure below).
f(x) for all nearby numbers x
(A, C, F, and L in figure below).
 c
c  d: see figure above.
d: see figure above.
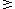 O , and f '(d)
O , and f '(d) O , then x = c is a relative maximum; again, see GRAPH A above.
O , then x = c is a relative maximum; again, see GRAPH A above. O , and f '(d)
O , and f '(d)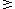 O , then x = c is a relative minimum; again, see GRAPH B above.
O , then x = c is a relative minimum; again, see GRAPH B above.
