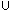Mathematics 143
Set Theory - Terms and Symbols
|
I. Set notations |
|
(a) |
Capital letters : A, B, C, S, T |
|
(b) |
Curly brackets containing a list of elements.
Example : {a, b, c} is the set containing the letters a, b, and c. |
|
(c) |
Set-builder notation (see Rolf Pg. 425).
Example : {x | x satisfies property P} where P is any property which makes sense
when applied to x. It may be either easy or difficult to determine whether or not
property P is true for certain values of x. If the determination takes a very
long time, such as a billion years, the set may have uncertain status. |
|
|
II. Special sets |
|
(a) |
U : The UNIVERSE SET, i.e., the set of all things (or elements) under
discussion at the moment. U changes from one problem to another. |
|
(b) |
Ø or { } :
the EMPTY SET or NULL SET, containing no elements. Note that { } is
different from the number "0" and the sets { 0 } and
{ Ø }. A common way to write
the number "zero" is to slash it, so that it differs from the letter "O",
but this practice must be avoided when the empty set enters a discussion.
|
|
|
III. Relations |
|
(a) |
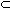 |
The following 6 statements all mean the same thing :
"A 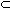 B" , "B B" , "B 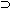 A" , A" ,
"A is contained in B", "B contains A", "A is a subset of B",
and "every element of A is an element of B". |
|
|
(b) |
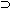 |
|
(c) |
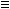 or = or = |
"A 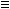 B" and "A = B" mean that the sets A and B have
precisely the same elements (as well as the same size). B" and "A = B" mean that the sets A and B have
precisely the same elements (as well as the same size). |
|
(d) |
/ |
means "not" when drawn across any symbol representing a verb. For example,
A  B means "A is not the same set as B" B means "A is not the same set as B" |
|
(e) |
e or  |
indicates set membership. Thus, "x e A" means that
"x is a member of the set A" or "x is an element of the set A". |
|
|
IV. Operations |
(a)  |
A  B = {x | x e A AND x e B} (See Rolf Pg 428 Fig 6-4) B = {x | x e A AND x e B} (See Rolf Pg 428 Fig 6-4) |
(b) 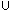 |
A 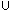 B = {x | EITHER x e A OR x e B} (See Rolf Pg 427 Fig 6-3) B = {x | EITHER x e A OR x e B} (See Rolf Pg 427 Fig 6-3) |
|
(c) A' or Ac |
A' = {x | x is not in the set A} (See Rolf Pg 429 Fig 6-6) |
|
(d) n(A) or |A| |
n(A) = is the size of A, or the number of elements in A. |
|
|
V. Venn Diagrams |
Venn Diagrams are stylized pictures of sets. See exercises |
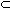
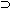
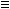 or =
or = 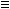 B" and "A = B" mean that the sets A and B have
precisely the same elements (as well as the same size).
B" and "A = B" mean that the sets A and B have
precisely the same elements (as well as the same size). B means "A is not the same set as B"
B means "A is not the same set as B"