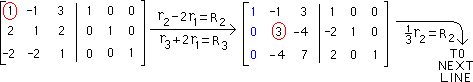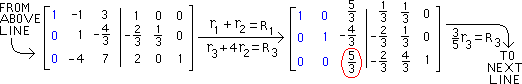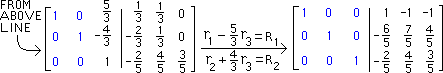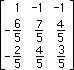THE INVERSE OF AN n x n MATRIX
|
See our text ( Rolf, Page 163) for a discussion of matrix inverses. Briefly, matrix
inverses behave as reciprocals do for real numbers : the product of a matrix
and it's inverse is an identity matrix. |
Let A be the name of our nxn matrix: non-square matrices have no inverse.
The following steps will produce the inverse of A, written A-1. Note the similarity
between this method and GAUSS/JORDAN method, used to solve a system of
equations.
| [2] |
|
Pivot on matrix
elements in positions 1-1, 2-2, 3-3, continuing through
n-n in that order, with the goal of creating a copy
of the identity matrix
In in the left
portion of the augmented matrix. |
|
If one of the pivoting elements is zero, then first interchange
it's row with a lower row. If no such interchange produces
a non-zero pivot element, then the matrix A has no inverse. This
step [2] is equivalent to step 2 on Pg 163 of our text Rolf,
resulting in (REDUCED) DIAGONAL FORM.
See an example below, and try the
Pivot Engine when you check your
pivoting skills. |
|
[ A | In ]
===> [ In
| A-1 ] |
|
|
| [3] |
|
When step [2] above is done, the right half of the latest
augmented matrix will be the desired inverse,
A-1; write it separately, and you're done,
as in the example below. |
|
| Note 1 :
|
Professor McFarland names
row operations just a bit
differently from our text: follow Prof McFarland's naming style. |
Note 2 : Check out Prof McFarland's
interactivePIVOT ENGINE
as you use row operations.
Note 3 : Compare the above 3 steps for
those used in GAUSS/JORDAN.
EXAMPLE OF FINDING THE INVERSE OF A MATRIX A
See our text (Rolf, Pg 163) for one example; below is another example :
|
We must find the inverse of the matrix A at the right |
|
| A = |
 |
1
2
-2 |
-1
1
-2 |
3
2
1 |
 |
|
|
| |
|
Below is the same matrix A, augmented by
the 3x3 identity
matrix. The first pivot encicled in red |
|
Below are the row operations required for the first
pivoting |
|
Next pivot on "3" in the 2-2 position below, encircled in red |
|
|
The columns of the 3x3 identity matrix are colored blue
as they re-appear on the left side |
|
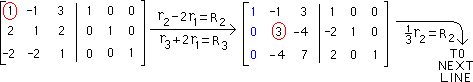 |
|
Below is the result of performing
P1, so the pivot
(2-2 position) is now "1". Next we perform
P2 |
|
Row operations
of P2
are below |
|
The result of the second pivoting is below. We now
pivot on the
element in the 3-3 position, encircled in red below |
|
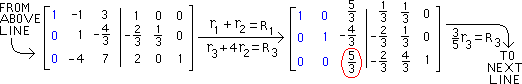 |
|
Below is the result of performing P1, so
the pivot (3-3 position) is now "1". Next we perform
P2. |
|
Below are the row operations of P2 |
|
The result of the third (and last) pivoting is below with
3x3 identity matrix in blue |
|
|
The matrix below is NOT A-1 |
|
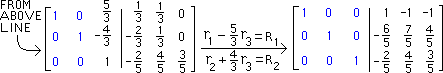 |
|
(REDUCED)
DIAGONAL
FORM
E |
|
Thus, our final step is to
separate the desired inverse
from the above matrix: |
|
|
A-1 = |
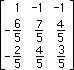 |
|
|
Note : THE MATRIX INVERSE METHOD for solving a system of equations will use
the above discussion, and even continue the above problem.