| Prof McFarland's Names | Row Operation | Text's Names | |||||
|
Interchange rows rm and rn |
|
|||||
|
|
c. Rm  Rm Rmor 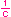 . Rm . Rm  Rm Rm |
|||||
|
Add a Multiple of Row n to Row m |
Rm + c. Rn  Rm Rm |
|
|
|
|
||||
|
|||||
|
| Prof McFarland's Names | Row Operation | Text's Names | |||||
|
Interchange rows rm and rn |
|
|||||
|
|
c. Rm  Rm Rmor 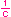 . Rm . Rm  Rm Rm |
|||||
|
Add a Multiple of Row n to Row m |
Rm + c. Rn  Rm Rm |
An example of how row operations should look is shown below, with all rows color coded (black/green/magenta/brown/blue) to show the match-up between matrix rows and their names.
 |
 3 |
-1 2 |
 |
2 11 |
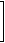 |
r2 - 3r1 = R2 |
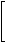 |
1 0 |
-1 |
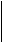 |
2 5 |
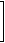 |
(0.2)r2 = R2 |
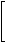 |
1 0 |
-1 1 |
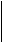 |
2 1 |
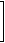 |
r1 + r2 = R1 |
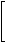 |
1 0 |
0 1 |
 |
3 1 |
 |
|
|
|
Once a pivot is chosen, the row operations of pivoting MUST BE AS FOLLOWS:
| P1 |
|
|
| P2 |
|
Note 1. The number changing to "1" is called a PIVOT, is usually encircled, and cannot be zero.
Note 2. Completely finish both P1 and P2 (above) before choosing another pivot.
Note 3. Prof McFarland has designed a time-saving interactive PIVOT ENGINE: check it out!
Note 4. (Again) Our brief example of pivoting, with row names color-matched with matrix rows:
 |
 3 |
-1 2 |
 |
2 11 |
 |
r2 - 3r1 = R2 |
 |
1 0 |
-1 |
 |
2 5 |
 |
(0.2)r2 = R2 |
 |
1 0 |
-1 1 |
 |
2 1 |
 |
r1 + r2 = R1 |
 |
1 0 |
0 1 |
 |
3 1 |
 |
Thus, in the example just above, there are actually TWO pivot transformations shown. One consists of the 1st row operation alone, whose pivot was the number "1" in the original matrix, encircled; the other consists of the 2nd and 3rd row operations as a pair, whose pivot is the encircled number 5.
| Note 5. | Use pivoting when possible during Gauss/Jordan (Rolf, section 2.2) and when you find matrix inverses (Rolf, section 2.6). Though pivoting is not required to obtain correct answers in these sections, pivoting WILL be required later during simplex method, and now is a good time to develop the habits needed at those later times. |