|
SIMPLEX METHOD OUTLINE FOR
STANDARD MAXIMIZING PROBLEMS |
|
|
The simplex method changes constraints (inequalities) to equations in
linear programming problems, and then solves the problem by matrix
manipulation. The solution set for the altered problem is of higher
dimension than the solution set of the original problem, but it is
easier to study with matrices. |
Reference : What is a STANDARD MAXIMIZING PROBLEM?
Reference : An example of SIMPLEX METHOD for a standard problem is available.
|
|
Rewrite each constraint (inequality)
as an equation (Rolf 8th ed., pg. 276) : See example? |
|
|
|
Write the revised problem as a tableau, with the
objective row (= bottom row)
consisting of negatives of the coefficients of the
objective function z ;
z will be maximized.
The lower right corner is the value of z when x, y,... are zero ;
thus, z usually starts out as zero.
See example? |
|
Reference: Some books (such as Rolf 8th ed., pg. 279) use an extra
"z-COLUMN" which never changes and will
be omitted in Prof McFarland's class. If you wish to use a
z-COLUMN,
this is OK: nothing else will be affected either way. |
|
Definition
|
The IDENTITY SUB-MATRIX (ISM) is an identity matrix
located in the slack variable columns of the starting tableau, but moving
to other columns during simplex method. This definition is not in Rolf. |
|
Definition
|
A BASIC SOLUTION for a tableau is a corner point of the
(unseen) solution set of the original system of inequalities.
For each tableau, the coordinates of its basic solution
are as follows (Rolf 8th ed., pg. 287, or
See example?): |
|
[a] All variables not associated with the
ISM are set equal to zero. |
|
[b] Evaluate other variables by reading each
tableau row as an equation. |
|
|
 |
"HOPPING" STRATEGY :
|
Simplex method will move the ISM, one column at a time; after each
such move, we arrive at (or "hop" to) a new corner point (basic solution) with
bigger objective value. Since the solution set has only finitely many
corners, this process ultimately yields the biggest value of the
objective function. |
INDICATORS: (not in Rolf)
|
An INDICATOR (for standard maximizing problems) is a
number in the bottom (objective) row of a tableau, excluding the
rightmost number. Thus here, the INDICATOR ROW is the bottom row, but
for non-standard problems the indicator
row will be a different row. |
FIRST FIND THE PIVOT: (Rolf 8th ed., pg. 294)
|
|
The pivot column is that column containing the most negative
indicator. If no indicator is negative, the tableau is a
FINAL TABLEAU : see step 8. |
|
Form RATIOS (quotients) for each row: divide the right-most number by
the number in the pivot column of that row. |
|
|
The PIVOT ROW is the row with the
smallest NON-NEGATIVE ratio (quotient).
Note that 0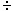 (+1) and 0 (+1) and 0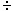 (-1)
are both numerically zero, but in calculating RATIOS,
consider 0 (-1)
are both numerically zero, but in calculating RATIOS,
consider 0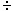 (+1) as positive (OK), and
0 (+1) as positive (OK), and
0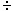 (-1) as negative (not OK). (-1) as negative (not OK). |
|
|
|
Apply a pivot operation (Rolf 8th ed., pg. 98) to
the tableau, including the bottom (objective) row. The pivot column
will become a column of a new ISM in the new tableau.
Note which column is replaced, and where the new ISM is located ;
its columns may not be in the usual order: not to worry. Check out
the PIVOT ENGINE to speed up practice. |
|
|
(optional) Note the new basic solution
(corner point) for the new tableau. |
|
|
|
If all indicators (in the bottom row) are non-negative,  :
your tableau is a FINAL TABLEAU. The basic solution of step 7
is the maximal solution you have been seeking! Note that if you correctly reached this
step from a Non-Standard Problem, then all
right-side numbers above the objective row will also be
non-negative. :
your tableau is a FINAL TABLEAU. The basic solution of step 7
is the maximal solution you have been seeking! Note that if you correctly reached this
step from a Non-Standard Problem, then all
right-side numbers above the objective row will also be
non-negative. |
|
|
Otherwise, if some indicator remains negative, repeat steps 3 through
9 WITH YOUR NEW TABLEAU. After a finite number of such repetitions
(usually 2-3), simplex method must terminate at step 8. |


 (+1) and 0
(+1) and 0 :
your tableau is a FINAL TABLEAU. The basic solution of step 7
is the maximal solution you have been seeking! Note that if you correctly reached this
step from a
:
your tableau is a FINAL TABLEAU. The basic solution of step 7
is the maximal solution you have been seeking! Note that if you correctly reached this
step from a 
