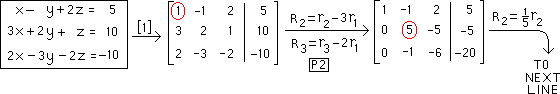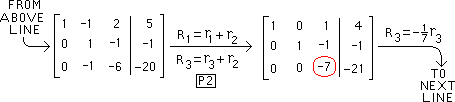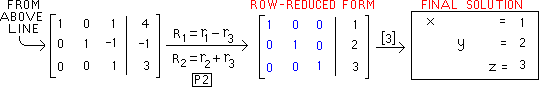The Gauss-Jordan Method
J. Gauss:
1777-1855		   M. Jordan:
1838-1922

GAUSS / JORDAN (G / J) is a device to solve systems of (linear) equations.
Given a system of equations, a solution using G / J follows these steps:

[1]
Write the given system as an augmented matrix.
Examples of this step are below
[system] ===> [ A | B ]
[2]
Use row operations to change A to an Identity Matrix, I:
This step can be done in many ways. A very systematic procedure can be viewed in Prof McFarland's Finite Math Website, but for this Algebra course, you are free to tinker in your own style, perhaps modelling your work on the example below.
[ A | B ] ===> [ I | C ]
[3]
When [2] is done, re-write the final matrix [ I | C ] as equations.
C will be a (vertical) list of variable values which solve the system, as in the example below

Note : Professor McFarland names row operations just a bit differently from our text.

One simple example of Gauss/Jordan appears with our list of row operations.
Below is a system
of equations which
we will solve
using G/J
step
1
Below is the
1st augmented
matrix: Note the
location of the
red-circled "1" in I3
Row
operations
named below
change column 1
into what we want
Next we change "5"
in the 2-2 position
encircled below.
This is where "1"
in I3 must be

  
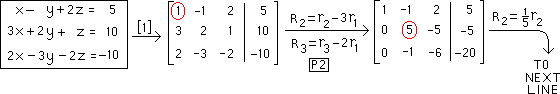Below is the result of
"R2 = (1/5)r2". The
element in the 2-2 position
has become "1" as in I3
Row operations
to change the rest
of column 2 are below
Column 2 below is now
what it is in I3.
Now alter the "7"
encircled in red
Using the row op
"R3 = (-1/ 7)r3"
below to change
"-7" to "1" as in I3
        
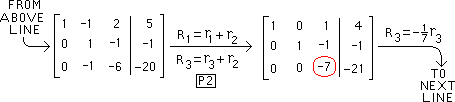Below is the result of
"R3 = (-1/ 7)r3".
Now we must change
the rest of column 3
Row operations
to change the
rest of column 3
are below
The result of all
row operations
is below, with
the identity I3
matrix in blue
Step
[3]
of
G/J
Re-writing the
final matrix as
equations gives
the solution to
the original system

Return to
Math 141
Home Page
   
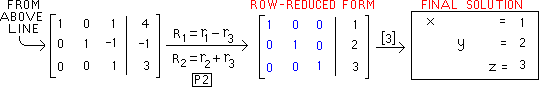This page last updated
22 July 1999