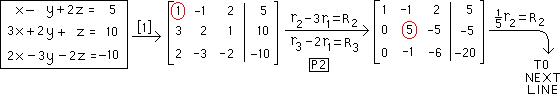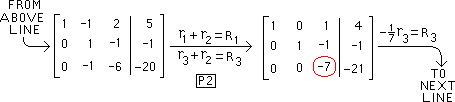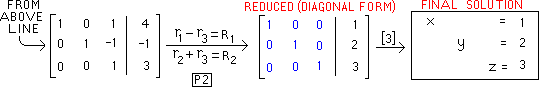The Gauss-Jordan Method
Row-reduced form
J. Gauss:
1777-1855		   M. Jordan:
1838-1922

GAUSS / JORDAN (G / J) is a device to solve systems of (linear) equations.
Given a system of equations, a solution using G / J follows these steps:

[1]
Write the given system as an augmented matrix.
Examples of this step are below, or in specialized example "b",
or in specialized example "c", or in our text Rolf (Pg 88).
 
[system] ===> [ A | B ]
[2]
Convert [ A | B ] to REDUCED FORM:
Pivot on matrix elements in positions 1-1, 2-2, 3-3, and so forth as far as is possible, in that order, with the objective of creating the biggest possible identity matrix I in the left portion of the augmented matrix. If one of these pivoting elements is zero, then first interchange it's row with a lower row. For all problems you will see this semester, this step [2] is equivalent to steps 1 through 7 on Pg 95-96 of Rolf, resulting in REDUCED FORM.
 
[ A | B ] ===> [ I | C ]
[3]
When [2] is done, re-write the final matrix [ I | C ] as equations.
C will be a (vertical) list of variable values which solve the system, as in the example below

Note 1: It is possible to vary the GAUSS/JORDAN method and still arrive at correct solutions to problems. For example, the pivot elements in step [2] might be different from 1-1, 2-2, 3-3, etc. Also, it is possible to use row operations which are not strictly part of the pivoting process. Students are nevertheless encouraged to use the above steps [1][2][3].

Note 2: Professor McFarland names row operations just a bit differently from our text:
follow Prof McFarland's naming style.

Note 3: Compare the steps of G / J with those for finding < a href="inverse.htm">matrix inverses.

One simple example of G/J row operations is offered immediately above the pivoting reference;
an example is below:
Below is a system
of equations which
we will solve
using G/J
step
1
Below is the
1st augmented
matrix : pivot
on the "1"
encircled in red
Row
operations
for the 1st
pivoting are
named below
Next we pivot on the
number "5" in the
2-2 position,
encircled below

  
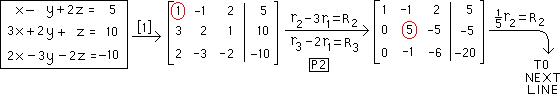Below is the result of
performing P1 on the
element in the 2-2 position.
Next we must perform P2
Row
operations
of P2
are below
The result of the 2nd
pivoting is below.
Now pivot on "-7"
encircled in red
Using P1
below
we change
"-7" to "1"
       
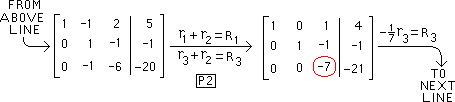Below is the result of
performing P1 on "-7"
in the 3-3 position.
Next we must
perform P2
Row
operations
of P2
are below
The result of the
third (and last)
pivoting is below
with 3x3 ISM
matrix in blue
Step
[3]
of
G/J
Re-writing the
final matrix as
equations gives
the solution to
the original system

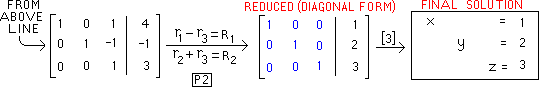To check your pivot calculations, try the PIVOT ENGINE.