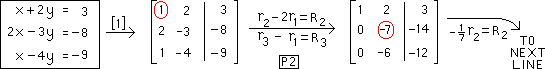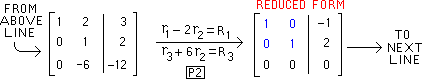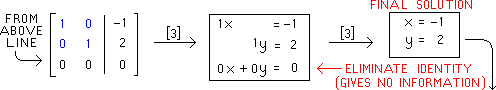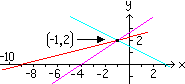When there are fewer variables than equations, we proceed just as we did in other examples of GAUSS/JORDAN. The GAUSS/JORDAN procedure will end, typically, in a matrix whose left part contains one or more rows of zeros. The student's dilemma, therefore, is how to interpret such rows of zeros. An example is below, with 3 equations and 2 variables; watch what happens, especially near the end :

To check your pivot calculations, try the PIVOT ENGINE.

Below is the system of equations which we will solve by G/J	step 1	Below is the 1st augmented matrix: pivot on "1" in the 1-1 position	row operations P2 for the first pivoting are named below	Next we pivot on the number "-7" in the 2-2 position, encircled in red below

---

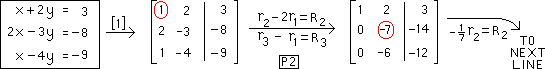Below is the result of performing P1 on the element "-7" in the 2-2 position. Next we must perform P2	The row operations of P2 are below	The result of the second and last pivoting is below. The remaining row contains only zeros, so the row operations of GAUSS/JORDAN are complete

---

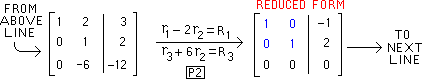Below is a copy of the final matrix of the previous line, with it's identity matrix in blue	We now re-write each row of this matrix as an equation, just as we wrote the original equations as a matrix	The 3rd row below corresponds to an identity, giving no information. Thus, we ignore row 3, basing a final solution on rows 1 and 2

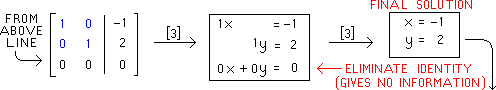IMPORTANT NOTE : If the 3rd row of the above solution had been "0x+0y=2", instead of "0x+0y=0", then the original problem would have NO SOLUTION, since "0=2" is always false. See also our text (Rolf): example 5 on page 113.

Recall our original system color-coded x + 2y = 3 2x - 3y = - 8 x - 4y = - 9

The 3 original equations are graphed below, showing the solution found by G / J above.
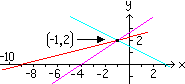