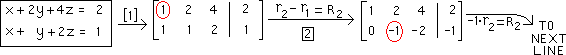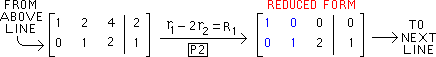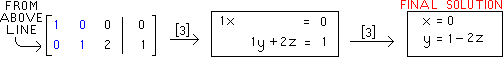When there are fewer equations than variables, we proceed just as we did in other examples of GAUSS/JORDAN. When the GAUSS/JORDAN procedure has ended, however, we are typically faced with infinitely many solutions. The student's dilemma is how to display such solutions. The problem below has 3 variables and 2 equations; watch what happens below, especially at the end:

Below is the system of equations which we will solve by G/J	step 1	Below is the 1st augmented matrix : pivot on the"1" in the 1-1 position	The one row operation for the first pivoting is named below	Next we pivot on the number "-1" in the 2-2 position, encircled in red below

---

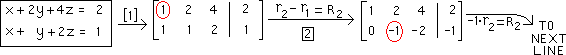Below is the result of performing P1 on the element "-1" in the 2-2 position. Next we must perform P2	The one row operation of P2 is below	The result of the second and last pivoting is below. There is no 3-3 position, so the row operations of GAUSS/JORDAN are complete

---

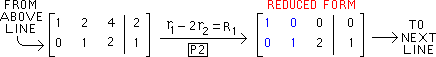Below is a copy of the final matrix of the previous line, with it's identity matrix in blue	We now re-write each row of this matrix as an equation, just as we wrote the original equations as a matrix	A traditional style for a final solution uses a parameter (here : z). Other variables are then written in terms of that parameter (as below)

To check your pivot calculations, try the PIVOT ENGINE.

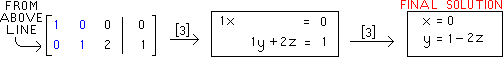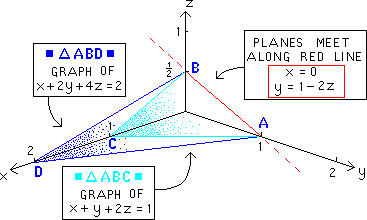
The FINAL SOLUTION above contains infinitely many points along the (RED) line AB below.
To get a sense for what this solution "means" Prof M^cFarland has drawn graphs below
of the original equations (blue and aqua planes below) and their red intersection :