THE DIAMOND MERCHANT
(completed solution)
Re-stated problem
|
A diamond merchant accidentally dropped 3 valuable
diamonds and 7 less valuable but similar zircons together
into a bowl. To separate the two kinds of gems, the
merchant must examine each with a hand lens. What is the
probability that the merchant will find the 3 diamonds
after 3 examinations? (obviously, two could never be
sufficient) |
| |
As before, we define a few useful events
|
Let D1= "a diamond is found on the 1st examination" |
|
Let D2= "a diamond is found on the 2nd examination" |
|
Let D3= "a diamond is found on the 3rd examination" |
|
Let Z1= "a zircon is found on the 1st examination" |
|
Let Z2= "a zircon is found on the 2nd examination" |
|
Let Z3= "a zircon is found on the 3rd examination" |
| |
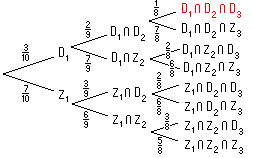
Conditional probabilities have now been assigned to all branches of the
tree which represents this problem. Using the Multiplication rule twice (Rolf Pg 537):
We seek P(D1
 D2 D2
 D3) D3) |
= P(D1) .
P(D2 | D1) .
P(D3 | D1 D2) D2) |
|
|
| = (3/10) .
(2/9) . (1/8) =
1/120 |
And now that you are aware of the methods in this solution, try answering
the following question about the same merchant and his/her bowl of ten
mixed gems:
What is the probability that after 3 examinations,
the merchant will have located exactly 2 of his 3 diamonds? |
|
|
Hint: all needed info is in the tree above |
| Give up? Try the: |
 |
|
 D2
D2




