THE DIAMOND MERCHANT
(solution to extra question)
Re-stated extra problem
|
A diamond merchant accidentally dropped 3 valuable
diamonds and 7 less valuable but similar zircons together
into a bowl. To separate the two kinds of gems, the
merchant must examine each with a hand lens. What is the
probability that after 3 examinations, the merchant will
find exactly 2 of the diamonds mixed with zircons? |
| |
As before, we define the same useful events
|
Let D1= "a diamond is found on the 1st examination" |
|
Let D2= "a diamond is found on the 2nd examination" |
|
Let D3= "a diamond is found on the 3rd examination" |
|
Let Z1= "a zircon is found on the 1st examination" |
|
Let Z2= "a zircon is found on the 2nd examination" |
|
Let Z3= "a zircon is found on the 3rd examination" |
| |
The conditional probabilities assigned to the above tree branches are the
same as were assigned in the previous version of this problem.
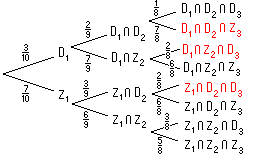
Notice that the red colored events in the tree
above are those for which exactly 2 of the 3 diamonds are found
after 3 examinations. We seek the probability of the UNION of these
three red events.
However, no 2 of these 3 red events can
happen at the same time: it is impossible to pick both a
diamond AND a zircon on the first examination, for example. Thus, the
three red events are mutually exclusive, and to
find the probability of their UNION, we add the separate probabilities
of the three red events. Indeed, each
of these red events is found exactly as
we found P ( D1
D2
D3 )
in the previous version of this problem,
using the multiplication rule twice (Rolf Pg 380):
| We seek P(D1
D2
Z3) +
P(D1
Z2
D3) +
P(Z1
D2
D3) |
| = P(D1).
P(D2|D1).
P(Z3|D1D2) +
P(D1).
P(Z2|D1).
P(D3|D1Z2) +
P(Z1).
P(D2|Z1) .
P(D3|Z1D2) |
| = (3/10) .
(2/9) . (7/8) +
(3/10) .
(7/9) . (2/8) +
(7/10) .
(3/9) . (2/8) |
| = (7/120) + (7/120) + (7/120) = 7/40 |
Note that as it turned out, all three red events had
the same probability (7/120), but this is a coincidence: other events
in the tree above have different probabilities.
 |
|
 |
This page last updated
2 June 2000 |
|
