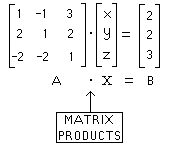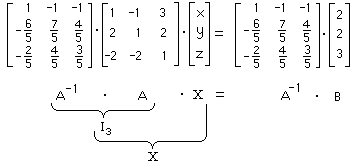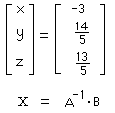MATRIX INVERSE METHOD
for solving a system of equations
See the similar discussion in our text, Rolf, on Pages 165-167 ;
the following continues an earlier discussion.
We start with a system of equations (right),
to be solved. The number of variables must equal
the number of equations, both equal to 3 here: |
|
| x |
- |
y |
+ |
3z |
= |
2 |
| 2x |
+ |
y |
+ |
2z |
= |
2 |
| -2x |
- |
2y |
+ |
z |
= |
3 |
|
|
On Prof. McFarland's tests, you would be asked
to solve the above problem
"by the matrix inverse method" in three distinct steps, as follows :
| [1] |
|
Write the given system (above) as a single matrix
equation: |
|
| |
|
Capital letter variables represent the matrices
(not numbers) which sit directly above them. Hence, the
above equation is a matrix equation.
Notice how the matrix entries correspond to
numbers in the original system of 3 equations |
|
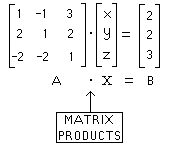 |
|
|
| [2] |
|
Solve the matrix equation obtained in
step [1] above; i.e., find X. |
|
|
In the MATRIX INVERSE METHOD
(unlike Gauss/Jordan),
we solve for the matrix variable X by
left-multiplying both sides of the above matrix
equation (AX=B) by A-1.
Typically, A-1 is calculated as
a separate exercize ;
otherwise, we must pause here to calculate A-1. |
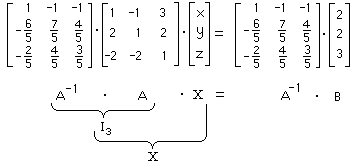 |
The left side (above) is easy to calculate
because an identity matrix
I
3 appears.
Note: A-1 is on the LEFT
side of both products. |
|
|
Step [2] is now completed by finding
A-1. B ===> |
|
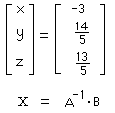 |
|
|
| [3] |
|
Using [2] above, write the solution to the
original system: |
|
|
original system |
| x |
- |
y |
+ |
3z |
= |
2 |
| 2x |
+ |
y |
+ |
2z |
= |
2 |
| -2x |
- |
2y |
+ |
z |
= |
3 |
|
|
|
|
|
solution to original system |
|
|
|
|
|