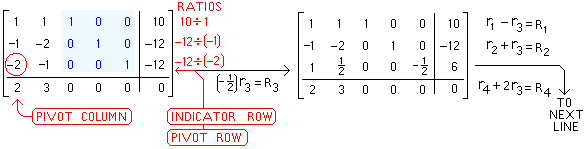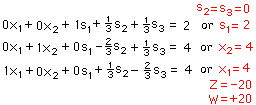a Simplex
EXAMPLE OF SIMPLEX PROCEDURE
FOR A NON-STANDARD
LINEAR PROGRAMMING PROBLEM
 
Below is
original
Problem
1st
step
"NS-1"
Red symbols
below were
changed by
step NS-1
2nd
step
"NS-2"
Red variables sn
below are called
SLACK VARIABLES
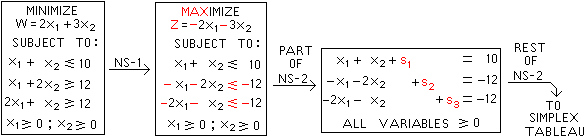There is a tie
for most negative
right-hand number.
Either "-12" is OK
The pivot in the
1st Simplex Tableau.
is circled below.
Missing Z-COLUMN??		 highlighted
is the
"ISM"
In the matrix
below, the
pivot has
become "1"
Named below are the 4
row operations needed
to pivot on the number
"-2" encircled in red
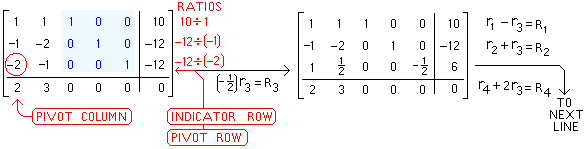Row operations
are named above;
their results
are below		 Highlighted
is the
new ISM
Since one right-hand
number (-6) remains
negative, we remain
in Phase I
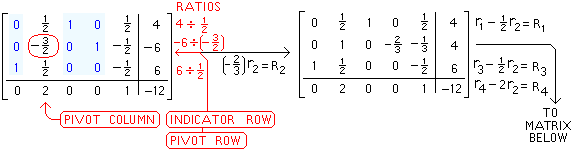
In the matrix
below, the
pivot has
become "1"
Named below are the 4
row operations needed
to pivot on the number
"-3/2" encircled in red
 
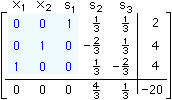
Row operations are named above; their results are at the right. The new ISM is highlighted. All right-most numbers above the bottom (objective) row are now zero or bigger; Phase I is now ended. Phase II now begins, presented as "Step 8" in Rolf (Pg 323)
 

In many non-standard problems, we would now find a negative indicator in the bottom row. However, in our last tableau above, a nice coincidence finds all indicators (0, 0, 0, 4/3, 1/3) are zero or bigger; "-20" is not an indicator. Hence, Phase II is completed at it's start, because the above tableau is a final tableau, and the row operations of SIMPLEX are done!

To obtain the final basic solution to our problem,
1st set equal to 0 each variable NOT associated with the highlighted ISM: variable tags are placed above each column in the final tableau.
2nd convert each row of the final tableau back into it's equation format, as at the right, to find the values of the remaining variables (shown in red).
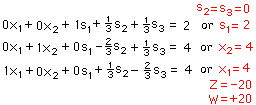