|
SIMPLEX METHOD
APPLIED TO MINIMIZING
and NON-STANDARD PROBLEMS |
|
Definitions
|
A linear programming problem (or linear program) is a set of
(linear) inequalities (with a solution set S) and a (linear)
function (often cost or profit) whose value (within S) is to be
maximized or minimized. |
|
|
A STANDARD MAXIMIZING PROBLEM is a linear programming
problem
which satisfies all of the following 4 CONDITIONS (Rolf, pg.263) : |
|
[C1] The objective function is to be maximized. |
|
[C2] All variables are non-negative. |
[C3] All inequalities are of the  type. type. |
|
[C4] All right hand constants are non-negative. |
|
|
Definition
|
A NON-STANDARD PROBLEM is simply a problem
which is not standard, and hence fails to satisfy at least one of [C1]
through [C4] above. In our text, [C2] is always true, which simplifies
discussions. |
|
 |
Reference : An example of how to apply the following procedure
to a non-standard problem is available, with abundant comments and cross-references.
Reference : Many EXERCIZES are available for each step of this
method.
|
|
Convert your problem into one satisfying conditions C1,C2, and C3
described above. How to do this is explained in Rolf 8th edition (pg 318-319). |
|
|
|
Convert all constraints to equations with slack variables, and then write the
problem as a tableau with some negative
right sides, with or without a Z-COLUMN. |
 |
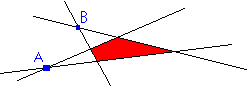
Strategy
|
The basic solution for a tableau with
some negative right sides is a point like A or B in the figure above
: it will not be a corner of the RED shaded solution set, but
rather will be an intersection of extended boundaries of that set. Our
first task will be to locate a corner point of the actual solution set
: this task might be called PHASE I
and is described here : it differs from the
procedure for a standard problem
only in STEPS NS-1 and NS-3. |
|
After locating some corner of the solution set (shaded above), we must
set out to locate the BEST corner : this second and final stage
of the solution is called PHASE II, and is
identical to the procedure for a standard problem. |
|
Note
|
PHASE I, as described in
Rolf 8th edition (Step 5, Pg 329), allows the freedom to choose any number as
pivot. On tests, you must follow the more restrictive
PHASE I procedure given below,
not the unrestricted procedure in Rolf. |
|
FINDING THE PIVOT
(steps NS-3 through NS-6)
|
Locate the row containing the most negative right-hand number. This row will be
called the INDICATOR ROW. If no right-hand number is negative, then your tableau
is STANDARD. |
 |
|
INDICTORS will consist of all numbers in the row found in NS-3, except the
right-most number; the PIVOT COLUMN will contain the most negative of these
indicators. If no indicator is negative, then there is no pivot column, and
the problem is unsolvable. |
 |
|
Form RATIOS or QUOTIENTS for all (non-objective) rows : for each row,
divide the right-most number by the number in the pivot column. |
 |
|
The PIVOT will be in the
ROW with smallest non-negative ratio.
Note that 0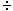 (+1) and 0 (+1) and 0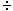 (-1)
are both numerically zero, but in calculating RATIOS, consider
0 (-1)
are both numerically zero, but in calculating RATIOS, consider
0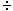 (+1) as positive (OK), and 0 (+1) as positive (OK), and 0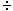 (-1)
as negative (not OK). (-1)
as negative (not OK). |
 |
|
If all right-most (non-objective row) entries are non-negative,
then phase I is ended. PHASE II now consists of
applying steps 3-9 of the standard maximizing
procedure to the new tableau obtained in step NS-7 above. Note:
PHASE II is described as step #7 on Page 329 of
our text, Rolf. |
|
Otherwise, if some right-most (non-objective row) entry is negative, apply
steps NS-3 through NS-9 to the new tableau obtained in NS-7. |






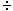 (+1) and 0
(+1) and 0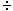 (-1)
are both numerically zero, but in calculating RATIOS, consider
0
(-1)
are both numerically zero, but in calculating RATIOS, consider
0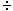 (+1) as positive (OK), and 0
(+1) as positive (OK), and 0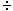 (-1)
as negative (not OK).
(-1)
as negative (not OK).
