|
SOLVING DIFFERENTIAL EQUATIONS |
|
|
EXAMPLES : |
[a] y' = 3x2 - 4
[b] y' = x y2
[c] y' = y'
| |
|
|
|
A DIFFERENTIAL EQUATION (DE) is an equation which "contains"
derivatives of some function. The word "contains" is not clearly defined :
does example [c] above "contain" y' ?? |
|
|
A function y(x) [ = y] is a
PARTICULAR SOLUTION
of a DE if the DE is a true statement about y. |
| |
As examples, y = x3 - 4x -1 is a particular solution of example [a] above,
-y-1 = ½ x2 is a particular solution of example [b] above,
and any function with a derivative is a particular solution of example [c] above. |
|
|
The
GENERAL SOLUTION of a D.E. is the set of all
of it's particular solutions, often expressed using a constant C
(or K) which could have any fixed value. |
| |
As examples, y = x3 - 4x + C is the general solution of example [a] above,
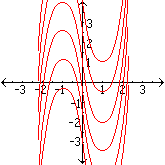
and -y-1 = ½ x2 + C is the general solution of example [b] above, shown as the collection of red graphs below. |
| |
| The collection of graphs of all particular solutions of a D.E. completely
fill up space, and no two graphs overlap, much as the layers of a dagwood sandwich. The red graphs in the
right image are playing the same role as the ham, cheese, and lettuce in Dagwood's sandwich in the left image. |
|
|
|
Many differential equations may be solved by separating the variables x and y
on opposite sides of the equation, then anti-differentiating both sides with respect to x.
When anti-differentiating the side containing y, the facts in the table below may be
useful. Each row of this table uses the chain rule or its alternate
statement integration by substitution (both with u = y)
|



 y'
y'