INTEGRATION BY SUBSTITUTION
(subtitle: the ANTI-CHAIN RULE)
Strategy
|
Integration by substitution allows changing the basic variable of an integrand
(usually x at the start) to another variable (usually u or v). The relationship
between the 2 variables must be specified, such as
u = 9 - x2. The hope is that by changing the
variable of an integrand, the value of the integral will be easier to determine. |
BASIC TOOL OF SUBSTITUTION
Form 1 of the basic tool
 |
g(x) |
du
dx |
dx = |
 |
g(u) du = G(u) |
|
|
Form 2 of the basic tool
 |
dy
du |
|
du
dx |
dx = |
 |
dy
du |
du |
= y |
|
|
|
using "g" as function name |
using "y" as function name
(resembles chain rule) |
The red differentials above indicate the variable used in the integrand:
"x" in the left-hand integral, "u" in the right-hand integral. The red "dx"
does not actually cancel with it's black counterpart, although it might
appear that way. The illusion of cancelling does provide a handy device
to remember the formula, however! See comments on isolated differentials.
WHEN DO I USE SUBSTITUTION ?
|
Try SUBSTITUTION when simpler methods alone have not been sufficient:
"simpler methods" include POWER RULE, SUM RULE, CONSTANT MULTIPLE RULE.
Look in the integrand (to the left of "dx") for two quantities, with one
(u')
equal to the derivative of the other (u):
see examples below. If you fail to see such a pair of quantities, abandon this
method. |
HERE ARE THE STEPS
(illustrated below)
- pick a value of "u" (the most common substitution variable name)
- Test your choice of u: (du/dx), or a constant multiple of it, must be a factor of the integrand as in Form 2 above.
If an adjustment multiple is needed, move it outside the integral. This step is in red
in examples below.
- The other factor of the integrand must then be (dy/du), to match the integrand in Form 2 above
- The desired anti-derivative (expressed using "u") is then the antiderivative of (dy/du) in step 3.
- Replace the "u" of step 4 above with what you chose in step 1 above.
|
| Example 1. Find |

|
1
x x x |
dx |
The color red represents u' and it's
values. Note the change of variable (from "x" to "u") after the 3rd equal
sign (green), using the
BASIC TOOL, in which
u' disappears.
Let u =  x x |
|
|
Thus y = |
 |
dy
du |
=  u u |
|
|

|
1
x x x |
dx = |

|
1
x |
1
 x x |
dx = |

|
u' |
1
u |
dx = |

|
1
u |
du =  u = u =  ( ( x) + C x) + C |
| Example 2. Find |

|
e-x |
dx |
The color red represents u' and it's
values. Note the change of variable (from "x" to "u") after the 4th equal
sign (green), using the
BASIC TOOL, in which
u' disappears.
|
Let u = -x |
|
|
Thus y = |
 |
dy
du |
= eu |
|
|

|
e-x |
dx = |

|
(-1)
(-1)
e-x dx = |
(-1) |

|
(-1)
e-x dx = |
(-1) |

|
(u ' )
eu dx |
= |
(-1) |

|
eu du |
= (-1)
eu =
- e-x
|
Example 3.
Again, The color red represents u' and it's values.
The "trick" (green) is common during integration by substitution.
The purpose is to generate a copy of u' so that the BASIC TOOL
above my be used to change from variable "x" to variable "u". Here we use "g" as the function name.
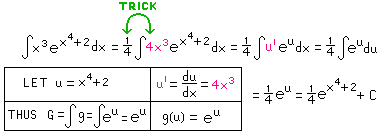
| Example 4.
(done without using isolated differentials)
Again, the color red represents u' and it's values. |
| Find |
 |
9(x2 + 3x + 5)8(2x + 3)dx |
|
 |
9(x2 + 3x + 5)8(2x + 3)dx = 9 |
 |
(x2 + 3x + 5)8(2x + 3)dx = 9 |
 |
u8 |
u' |
dx = 9 |
 |
u8du = |
|
|
LET u = x2 + 3x + 5 |
THUS
u
'
=
2x + 3 |
|
Thus y = |
 |
dy
du |
= |
 |
u8du = (1/9)u9 |
|
|
|
= 9 (1/9)u9 = u9 = (x2 + 3x + 5)9 + C (1/9)u9 = u9 = (x2 + 3x + 5)9 + C |
Example 5. (done without isolated differentials)
Again, The color red represents u' and it's values;
purple is used for y '
and it's values.
Note that the simplicity of u and u' can
actually make the solution harder to discover?? Compare this solution with a
different solution of the same problem; the
two differing methods appear to produce different answers. Can you show
these answers are equal, using only algebra?

 x
x x
x
 u
u
 x
x
 x
x

 u =
u =  (
( x) + C
x) + C






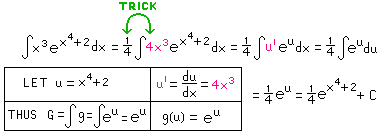







 (1/9)u9 = u9 = (x2 + 3x + 5)9 + C
(1/9)u9 = u9 = (x2 + 3x + 5)9 + C
 (x+1)8dx =
(x+1)8dx = 
 (x+1)8.1dx =
(x+1)8.1dx = 
 u8
u8 u' dx =
u' dx =
 u8 du =
u8 du =


 u8 du
u8 du u8
u8
