ISOLATED DIFFERENTIALS
 (a warning not to use them)

A DIFFERENTIAL is a symbol with 2 letters, the 1st being "d", the 2nd usually x, y, z, t, u, or v. Examples of differentials in proper context are below:

dx

dy		      du

dv		      dx

dt		      du

dx		     
f (x) dx
    
f (u) du

The differentials above behave like the letters spelling a word: the letters do not have separate meaning! Thus, "Robe" is a perfectly fine word, but the "Robe" in "Roberta" or "Robert" does not have the same meaning!! Similarly, "du/dx" does NOT mean "du divided by dx"; the "cancellation" below is equally foolish:

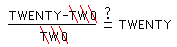
An ISOLATED DIFFERENTIAL is a differential which (like a fish out of water) does not occur in it's proper context, as part of a derivative or integral.

Examples of isolated differentials
du = 2x.dx
dv = dx

2x
3.du = 4.dx
Same 3 Examples re-written properly
du
dx		  = 2x
dv
dx		  =   1 
2x
du
dx		  =  4
3

Many texts (including ours) occasionally use isolated differentials, since they lead (rather mindlessly) to correct answers. However, using differentials in their proper context leads just as easily to correct solutions. Examples of the correct use of differentials may be found in the following web pages:

Integration by Substitution

Integration by Parts

It will be FORBIDDEN to use isolated differentials on tests.
It is always possible to express yourself just as easily without using them.

   
This page last
updated 5 January 2003