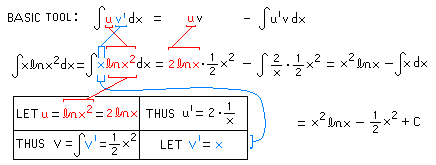Integration by Parts

INTEGRATION BY PARTS (IBP)
(subtitle: the ANTI-PRODUCT RULE)

The BASIC TOOL (from our text Hoffmann)

f(x) g'(x) dx = f(x)^.g(x) - f '(x) g(x) dx

Prof. M^cFarland prefers an equivalent statement found in many texts. The following popular form of our BASIC TOOL is easier to remember:

The BASIC TOOL: alternate form

u v' dx = u^.v -

u ' v dx

If one differentiates both sides of either equation above, the result is the PRODUCT RULE for derivatives, hence the name "ANTI-PRODUCT RULE".

The understanding in both forms is that "x" is the basic variable of all functions:
f(x), g(x), and also u and v.

WHEN DO I USE INTEGRATION BY PARTS ?
Try INTEGRATION BY PARTS when all other methods have failed: "other methods" include POWER RULE, SUM RULE, CONSTANT MULTIPLE RULE, and SUBSTITUTION. For this method to succeed, the integrand (between and "dx") must be a product of two quantities: you must be able to differentiate one, and anti-differentiate the other. Also, after applying the BASIC TOOL above, the new integral you obtain should be easier to evaluate than the original. If any of these requirements is not met, abandon your choice of u and v' and be prepared even to abandon this method.

WHEN DO I USE INTEGRATION BY PARTS ?
Try INTEGRATION BY PARTS when all other methods have failed: "other methods" include POWER RULE, SUM RULE, CONSTANT MULTIPLE RULE, and SUBSTITUTION. For this method to succeed, the integrand (between and "dx") must be a product of two quantities: you must be able to differentiate one, and anti-differentiate the other. Also, after applying the BASIC TOOL above, the new integral you obtain should be easier to evaluate than the original. If any of these requirements is not met, abandon your choice of u and v' and be prepared even to abandon this method.

Example 1. (Hoffmann, Pg 425, #6) In the following presentation, the choices for u and v' must be made at the start. These are color-coded, and the BASIC TOOL (copied from above) is positioned nearby for comparison. Notice that isolated differentials are not used in this solution.

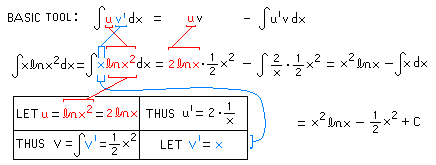
Example 2. Compare this solution with a different solution of the same problem. Especially, note that the 2 differing methods appear to produce different final answers. However, it is possible to show the two answers are indeed equal, by algebraically altering their forms.

x^.(x+1)⁸dx

x^.(1/9)(x+1)⁹

1^.(1/9)(x+1)⁹dx

(1/9)x(x + 1)⁹ - (1/9)(1/10)(x+1)¹⁰ + C

u ^. v' dx

u ^. v

u' ^. v dx

All work is color-coded so equal
numbers have the same color

LET u = x

THUS u' = 1

THUS v =

v' =

(x+1)⁸dx = (1/9)(x + 1)⁹

and let v' = (x+1)⁸

Try interactive self-test?

This page last
updated 14 March 2001