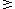The above information is from your computer : be sure it is correct.
For grade credit, submit over the internet by 11:59 PM (= 23:59 hours) on Sunday 13 March 2016 |
| [1] |
At the right are 5 lines: the 2 axes and 3
others in color. These lines include the graphs of the
equations associated with the inequalities
boxed below. Click any or all boxes(s) which are located in the solution
set of the system of inequalities boxed below.
On paper tests, students will be asked to
create these graphs without a graphing calculator. |
|
|
|
x |
+ |
2y |
 |
62 |
|
4x |
+ |
y |
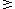 |
66 |
x 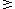 0 0 |
; |
y 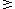 10 10 |
|
|
|
|
| [2] |
|
(a)(3 points) Find the coordinates of all 3 corner points of the solution set which
you identified as an answer to [1] above. Enter these coordinates in the top row below. |
(b)(2 points) Find the value of the objective function [P = x + 3y] at each
of the 3 corners in [2a] above. Enter these values in the bottom row below.
Scoring : You must first earn a perfect 5 pts in [1] and 3 pts in [2a],
1 pt for each corner point. [2b] is then scored "all or nothing" |
|
(c) (unscored) Note where P has its biggest value. |
|
| [3] |
Consider the problem in the box below : without solving it. |
|
The Kane Company makes two models of
grills, one gas and one electric. Each gas grill requires 3 pounds of
iron and 6 minutes of labor; each electric grill requires 4 pounds of
iron and 3 minutes of labor. Kane must produce at least 150 gas grills
to fill a backlog of orders for this model only. Each gas grill yields
a profit of $2, and each electric grill yields a profit of $3. Kane has
a supply of 1000 pounds of iron, and 20 hours of labor
available. How many grills of each type should Kane produce in order
to maximize it's profit? |
|
|
Just set this up. |
 |
|
|
|
|
| |
(a)(3 pts) In the box below are various ways to define variables in solving the above problem.
Choose one or more of these definitions of variables, so that taken together, your
choices would be the best in solving the problem above.
On paper tests, you must write definitions rather than choose among options.
Scoring: 2 points for variables x and y, one point for the objective function (capital letter) |
|
|
| |
(b)(2 pts) Using the best definition of variables from the choices in
[3a] above, choose one or more of the options below to
assemble a correct translation of the original problem into
a set of inequalities and objective function below.
You must first earn a perfect 3-point score on [3a] above in order to earn points in [3b].
Scoring below : Inequalities worth 1½ points, objective function worth ½ point |
| |
|
| [4] |
For the linear programming problem in the box
(at the right), do as follows:
For each of the 6 lines of the problem in the box, click either
NON-STANDARD or STANDARD, depending upon whether or not one of
the four conditions for a standard problem are violated. These
4 conditions appear above problem [7] on this test. |
|
|

I can help |
| [5] |
Enter numbers of the SIMPLEX TABLEAU ( = ST ) for the problem at the right.
Continued in [6] below.
Scoring : bottom row worth 3 points, remaining 2 rows worth 1 point each |
Maximize P = 4x1 + 6x2
subject to : |
|
x1 |
+ |
2x2 |
 |
24 |
|
3x1 |
+ |
x2 |
 |
8 |
x1 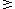 0 0
x2 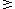 0 0 |
|
|
|
|
|
| [6] |
|
Use THE SPECIFIC STEPS
OF SIMPLEX METHOD OUTLINED IN OUR CLASS HANDOUTS to solve problem [5] (in box at right).
WITH CORRECT WORK, you will encounter one pivot and no fractions. As in our text, two
Slack Variables will be named s1 and s2 . |
On tests given in class, the test-taker must also write the matrices,
since without them, the 2 needed row operations and basic solution
( 7 answer boxes below) cannot be discovered.
Scoring : You must get a perfect (5 pt) score on [5] above before trying [6].
Then for [6] : 1 point for each row operation (left box) ; 1 point for each row of the basic solution (right box) |
|
|
Final basic solution :
 |
|
|
|
|
| [7] |
See alternate sample test as example of what [7][8][9] on your paper test will look like.
Here (for 5 points), you must only enter the numbers of the SIMPLEX TABLEAU, as in [5] above.
Scoring : bottom row worth 3 points, each other row worth 1 point |
|
|
| [8] |
(6 points) Use SPECIFIC STEPS OF
SIMPLEX METHOD OUTLINED IN OUR CLASS HANDOUTS, to solve the problem in [7] above.
Enter numbers in decimal form to complete the needed 6 row operations below.
With correct work, you will encounter 2 pivots (3 row operations in each), both in
phase I of the
simplex method, at which point you will arrive at a FINAL TABLEAU.
All fractions in your matrices will have denominators 2,5, or 10:
no others; thus, decimals will terminate after one decimal place.
Scoring : You must earn a perfect 5 points in [7] above
before earning any points in [8]. One point for 1st row op ; three points
for the first 3 row ops ; 4 points for the first 4 row ops ; 6 points for all row ops.. |
| [9] |
(4 pts) You encountered 3 simplex tableaus in [8] above (starting, middle, and final), not counting intermediate
matrices. The basic solution for the starting tableau is : x1 = x2 = 0, s1 = -2, s2 = -3, z = w = 0.
Name the values of each of these variables for the middle and final tableaus: see diagram below.
Scoring : 2 points for each fully correct basic solution |
| |
Starting
basic solution :
x1 = 0 ;
x2 = 0
s1 = -2 ;
s2 = -3
z = w = 0 |
|
1st pivoting
 |
|
2nd pivoting
 |
|