Math 250 Business Calculus
This is Paper Test # 2 [Go to web quiz 2]
Numerical answers are in our text, Hoffman 11th ed.;
Methods will be discussed using other problems
Links to other web pages were not on original test;
CAUTION: Prof McFarland makes new tests each semester.
Math 25O Test 2 (Hour Exam : perfect = 45) given Fall 2017
Credit given in proportion to the clarity of your WORK
You need not evaluate anything beyond a point where a calulator is necessary |
__________________
PRINT name above |
|
|
|
Average grade on this test : 30.35 |
|
|
|
| [1] |
(Handout #1: c,e,n,u,v)(1 pt each) If f(x) = 3x + 2 and g(x) = x2 - 1,
enter integers (such as 7, 1, 0, or -4) to find: |
| |
(a) f( -1 ) = |
|

functions : almost
as useful as cats |
| (b) f(x - 1) = |
|
| (c) g(- 1) = |
|
| (d) g(f(x)) = |
|
| (e) g(g(x)) = |
|
| [2] |
(a)(Pg 40 #23)(2 points) Write an equation of the line with slope ( -½) passing through points (5, -2) by entering numbers below : |
| y = |
|
x + |
|
|
(enter numbers in boxes) |
|
|
(b)(Pg 93 #16a)(3 pts) Display ALGEBRA work used to discover the point of intersection of the graphs of
[ y = x2 - 1 ] and
[ y = 1 - x2 ].
Check by substitution does not count as "algebra". |
| [3] |
|
(#5 Pg 56) A farmer plans to build 1000 meters of fence to protect
a rectangular field. If one side of the field abuts a river and
does not require fencing, express the area A of the field
in terms of its width x (see figure). |

x |
|
|
|
|
| [4] |
|
(a)(Pg 75 #17)(3 pts) Find the limit or claim the limit does not exist : |
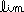 |
x  1 1 |
|
|
x2 - 1

x - 1 |
. |
|
| |
|
(b)(Pg 131 part of #67)(2 pts) The carbon monoxide concentration in Whitewater's
air is
Y = 0.05x2 + 0.1x + 3 ,
where x is the number of hours after noon. Find Y ', and
find the rate at which Y is changing at 1 PM. |
| |
| Y '(x) = |
|
x2 + |
|
x + |
|
|
[The rate at which Y is changing at 1 PM] = |
|
|
|
| [5] |
(Pg 114 part of #5) Use the LIMIT METHOD to find f '(x) if
f(x) = 2x2 - 3x - 5.
The answer is that f '(x) = 4x - 3, but
DO NOT USE "QUICKIE" RULES (such as the power rule) to find f '(x).
Also, you must correctly use limit notation at least twice for
full credit (see problem [4] above as an example). This is the only exam problem requiring the limit
method to find f '(x). |
| [6] |
|
(Handout, and Pg 128 #25) For this question , DO NOT use the limit method,
or the product rule, or quotient rule. No credit if
you use any of these 3 methods. |
| (a)(1 pt) |
Find f '(x) if f(x) = - |
x2

16 |
+ |
2
x |
+ |
x
3 |
|
 |
"I do these in my sleep,
but you be careful:
and stay awake |
|
| (b)(2 pts) |
Find f '(x) if f(x) = 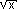  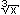 |
|
| (c)(2 pts) |
Find f '(x) if f(x) = |
|
|
|
|
For the remaining problems on this test, you may use any rule or method for
full credit, including the product and quotient rules. The limit method should
be avoided because it would be very difficult to use properly.
Showing your methods clearly may save you points. |
| [8] |
(Pg 181 #13 simplified) Use implicit differentiation to find
y' (the first derivative of y)
if
y2 + xy - 3x + 1 = 0 .
Thus, do NOT first solve for y (it would be hard), but rather : differentiate
both sides of the given equation. Your answer to [8] must be an
equation with y ' alone on the left side ;
the right side of your answer
will contain the variables x and y, but must not contain y' . |
| [9] |
(Pg 157 #57) Find y",
if y = (x2 + 5)8. (showing lots of work, since answer is given) |
|
The answer you are likely to write is : y" =
16(x2 + 5)7 + 224x2(x2 + 5)6 |

