The above information is from your computer : be sure it is correct.
For grade credit, submit over the internet by 11:59 PM (= 23:59 hours) on Sunday 14 February 2016


Enter your name above
Enter preferred email address;
include @ and whatever follows
Enter student I.D.
Math 76O-143 Finite Mathematics
Self-grading homework assignment #2
Submit over the internet by 11:59 PM on Sunday 14 February 2016
Maximum value toward semester grade is 4 pts
(Algebra, Compound Interest, and Matrices)
Links to other web pages were not on original test;
Methods will be discussed using other problems
CAUTION: Prof McFarland makes new tests each semester.
When you are finished,
send this to your Professor
Average grade on
Fall 2015 paper test #2 : 32.22		 Perfect score = 45 See future grade prospects?
[1] (a)(1 pt) Name the slope of the line with equation 4x + 2y = 14:
(b)(2 pts) Find an equation for the line through (-2,0) and (0,-4).
(a) -2x - 4y = 0
(b) x = -2 and y = -4
(c) y = -2x - 4		 (d) 2x = 4y
(e) x = -2
(f) y = -4
  (c)(2 pts) At the right is the final matrix when solving (by Gauss/Jordan) a system of 4 equations in variables x, y, and z. What can be said of the solutions to the system from which this matrix came?
1
0
0
0		 0
1
0
0		 0
0
1
0
2
-1
4
1
  (a) The solution is an identity
(b) x = 2, y = -1, z = 4
(c) x = 2, y = -1, z = 4, w = 1		 (d) 2x -y + 4z = 0
(e) There are infinitely many solutions
(f) There are no solutions
[2] TMI, Inc., makes blank CDs. TMI's fixed costs are $12,100. Each CD costs $0.60 to make, and sells for $1.15. Enter numbers in decimal form below expressing TMI's cost C (2 pts), revenue R (1 pt), and profit P (2 pts) when it makes x CDs.
[ Thus, if you (wrongly) thought C = ( ½ )x , you would enter 0.5 in the top left box and 0 in the top right box ]
Scoring : C and P worth 2 points each ; R worth 1 point
  C = x + ;
  R = x + ;
  P = x + .
[3]
Name the point where these lines intersect :
[enter decimal numbers at the right ]
2x - 3y = 6
3x + 6y = 16
The intersection is ( , )

For the following 3 questions [4][5][6], you must name the formula you plan to use (for 3 points), and then enter the answer to the question (for 2 added points).
On paper tests, these instructions will be somewhat different. See an example ?.
Your available choices of formulas (not given on original test) are:
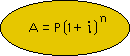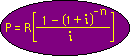Formula #1 Formula #2 Formula #3

Failure to practice this kind of problem accounted for
more lost points than any other problem type on this test
Scoring : Formula worth 3 pts ; numerical answer worth an added 2 pts (zero pts if formula is wrong)
[4] Bart is about to receive money in a trust started by a royal relative 21 years ago (at Bart's birth). If $2100 was originally placed in this trust, how much will Bart receive today, if the trust has earned 8% per year compounded quarterly? (See instructions above)
Formula #1
Formula #2
Formula #3		   Enter the amount Bart will receive: $
[5] The Taylors have a 30-year home mortgage to secure a home loan of $100 000. If annual interest rates are 6% compounded monthly, what is the Taylors' monthly mortgage payment?
Formula #1
Formula #2
Formula #3		   Enter the Taylor's monthly payment: $
[6] For the past 12 years, Julie's employer has contributed $1OO at the end of each month into a retirement account paying interest at an annual rate of 6% compounded monthly. How much is in Julie's account now?
Formula #1
Formula #2
Formula #3		   Enter the amount in Julie's account now: $
[7] (a)(2 pts) Write as a single matrix :
[Original matrices had a 3rd row ]		  
2
-1
3		 2
-2
- 3
-3
2		 1
-2
=


   (b)(3 pts) Find this matrix product :  
-1 2
3 1
2 4
3 1
=


Need help with matrix products ?
[8] Use GAUSS/JORDAN method to solve the system below left, clearly writing all row operations BETWEEN the affected matrices, and using the format     rn + k . rm = Rn or k . rn = Rn to name the row operations, where Rn is the name of the (new) row being built, and rn or rm are the name(s) of rows in the (old) existing matrix. Note that this naming scheme is the one used in examples done during class. If your work is correct, your matrices will contain NO fractions; each step of your work should look as below right :
x - 2y + z = 6
2x + y - 3z = -3
x - 3y + 3z = 10
 
old matrix
row op name
new matrix
Need help doing
row operations?
the Pivot Engine
Complete the row operations below needed to solve the above system by Gauss-Jordan. On paper tests, you must also write the matrices. On this digital exercise, write matrices on scratch paper, since without them, the 7 needed row operations ( 7 answer boxes below) cannot be discovered. A similar example is in this link
Scoring as follows : [first 2 row ops = 1 pt], [first 3 row ops = 2 pts], [first 5 row ops = 3 pts], [all 7 row ops = 5 pts]
 
starting
matrix
r2 + r1 = R2

r3 + r1 = R3
second
matrix
r2 = R2
third
matrix
r1 + r2 = R1

r3 + r2 = R3
fourth
matrix
r1 + r3 = R1

r2 + r3 = R2
final
matrix
[9] (a)(3 pts) Find A-1 for the matrix A below, using row operations. Name each row operation as described in [8] above. You will encounter a few fractions with denominator of "7" but no other fractions. Answer is given, so credit is only for WORK.
A = 
1 -2
2 3
   and your answer will be
A-1 = 
3
7		 2
7
   2
7		 1
7
Complete the row operations needed to find A-1 by entering numbers in the 3 text boxes.
On paper tests, you will also need to write the matrices. A similar example is in this link.
Scoring: [first row op = 1 pt], [first 2 row ops = 2 pts], [all 3 row ops = 3 pts]
 
starting
matrix
r2 + r1 = R2
second
matrix
r2 = R2
third
matrix
r1 + r2 = R1
final
matrix

    (b)(2 pts) Write the system of equations at the right
as a single matrix equation: A.X = B
  x - 2y =  3
2x + 3y = -8

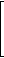All 8 boxes must be correct for 2 pts (no partial credit)
 



=

  
(c) (zero pts) On classroom tests the student must also find the solution to the system in [9](b) above by calculating X = A-1.B, using the matrices A-1 and B from [9](a) and [9](b). This skill is not tested here.

Comments or complaints regarding this page

HOW COULD THIS HOMEWORK ASSIGNMENT AFFECT MY COURSE GRADE?
Press the "display scoring" button to check your score before submitting :

When you have done your best above, send homework to your Professor HERE (below).
Be sure your email address is correct above: your graded homework will be immediately copied there.

Re-load page for new fortune