Math 76O-250 Business Calculus
This is Paper Test # 6 [Go to web quiz 6]
Numerical answers are in our text, Hoffman 11th edition;
Methods will be discussed using other problems.
Links to other web pages were not on original test;
CAUTION: Prof McFarland makes new tests each semester.
|
Math 250 Test 6 Fall 2017 |
|
|
Average grade on this test : 31.51 |
|
|
|
|
|
|
__________________
PRINT name above |
|
|
|
Yikes !
a calc test just before Christmas
? |
|
[A] Except perhaps for problems [2], [7], [9], put answers/work in blue book
[B] Credit given in proportion to the clarity of your WORK
[C] Use no isolated differentials. E.g., do not write "dy = 3xdx"
[D] You need not evaluate anything beyond a point where a calulator is needed
[E] NON-GRAPHING use of calculators is permitted |
|
| [1] |
(a)(#31 Pg 420)(3 pts) Find |
 |
( x-2 + x-3 ) dx |
|
| |
(b)(#31 Pg 420 cont'd)(2 pts) Show that |
 |
|
( x-2 + x-3 ) dx = |
4

18 |
or |
2
9 |
| [2] |
(part of #7 Pg 450) On the figure at the right is the
graph of [ y = 128 - 2x2] . |
|
(a)(1 pt, and hint to [2b]) Find the value of d shown on the graph. |
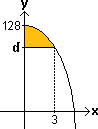 |
(b)(4 pts) Express the area shaded at the right as a single definite
integral by entering specific integers (such as 3, -2, or 0) in the 5 empty
answer boxes below. Note that in the original version of this problem, the
shaded area (which is not drawn to scale at the right) was a "Consumer's Surplus".
 |
|
( |
|
x2 +
| |
x +
| |
) |
dx |
|
|
| [3] |
(a)(Pg 438 #35 using function in Pg 420 #27)(3 pts) Luke can swim at the rate of
S = 2 + 2x + 3x2 (meters per minute) after being
in the pool for x minutes. What is the average value of S from x=2
to x=5? (Answer is about 50 m/min; show anti-differentiation work)
|
|
| |
|
(b)(#13 Pg 786)(2 pts) For the geometric series |

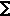
n=0 |
2
3n |
, write |
|
(for 1 point) its first 4 terms, and (for 1 more point) the sum of all its terms. |
|
| [4] |
|
(a)(3 pts)(#23 Pg 704) Find the GENERAL SOLUTION of the differential
equation y' = xy-2 |
|
| |
Your answer will be an equation with no "x" on the left side,
and no "y" on the right side.
Your answer should not contain y' and will
contain a constant symbol "C", for example, "y2 = x3 + C". |
| |
(b)(2 pts)(#23 Pg 704) In the answer to [4a] above, find the value of "C" for which y=3 when x=2 |
| [5] |
(a)(#1 Pg 515)(3 pts) Find |
 |
 |
| |
| 1 |
|
1
x3 |
dx , or state that the integral diverges (does not exist) |
|
|
|
|
(b)(#36 Pg 786)(2 pts) Write the repeating decimal
0.405405405.... as a reduced fraction of integers,
like |
13
41 |
|
| [6] |
(#5 Pg 584, voted in) Use least squares method to find the line best
fitting the data points :
(1,2) , (2,2) , (2,3), and (5,5) |
| [7] |
(a)(Pg 572 #7)(2 pts) Find fx , fy , fxx ,
fxy , and fyy where
f(x,y) = 2x3 + y3 + 3x2 - 3y - 12x - 4 . |
|
(b)(more of Pg 572 #7)(1 pt) Use fx and fy
above to find all 4 critical points (CP's) for the function
f(x,y) in (7a) above; enter these in the table below. |
|
(c)(rest of Pg 572 #7)(2 pts) Complete the table below
using your results in (7a) and (7b) above: |
| CP |
A = fxx |
B = fxy |
C = fyy |
D = AC - B2 |
Kind of CP:
Relative Maximum,
Relative Minimum,
or Saddle Point? |
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
|
|
[8](a)(part of Pg 618 #13)(3 pts) Evaluate (showing work) |
 |
|
(2x + y) dx |
 |
May I present
the answer to [8a]:
namely 2y - 2y2 |
|
|
(b)(Rest of Pg 618 #13)(2 pts) Evaluate the double integral:
|  |
|
 |
|
(2x + y) dxdy ; answer is |
1
3 |
The algebra and calculus (above) are fairly easy. Credit given only for work.
Note [C] at top of test.
|
| [9] |
(a)(on syllabus)(3 pts)Fill in the
table at right for the function
f(x) = 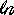 (x+1) (x+1) |
| |
(b)(2 pts) Use your table entries
(at the right) to write the
first four terms of the
Taylor series about (a=0) for the
function f(x) = 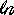 (x+1) (x+1) |
|
| n |
function: f (n)(x) |
value at
x = 0 |
an
|
| 0 |
|
|
|
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
|


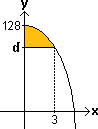



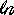 (x+1)
(x+1)
