Math 250 Business Calculus
This is Paper Test # 4 [Go to web quiz 4]
Numerical answers are in our text, Hoffman 8th edition;
Methods will be discussed using other problems
Links to other web pages were not on original test;
CAUTION: Prof McFarland makes new tests each semester.
Mathematics 25O Test 4 (Hour Exam : perfect=45) given Fall 2017
[A] Credit given in proportion to the clarity of your WORK
[B] You need not evaluate anything beyond a point where a calulator is necessary
[C] NON-GRAPHING use of calculators is allowed |
__________________
PRINT name above |
|
|
|
Average grade on this test : 27.83 |
|
|
|
| [1](a) |
(#13 Pg 228 and web quiz 3 ; see [2] below?)(1 pt) Find f '(x)
if f(x) = |
1
3 |
x3 - 9x + 2 : |
|
|
(Enter numbers in boxes) f '(x) = |
|
x2 + |
|
x + |
|
; |
|
|
| |
|
(b)(4 pts) Find both CVs (critical values) for f(x) in [1a]
above. Then test each CV by filling in the
7 empty boxes of the table (right). |
|
 |
test value |
smallest
CV |
test value |
largest
CV |
test value |
| x |
-4 |
|
0 |
|
5 |
| f '(x) |
|
0 |
|
0 |
|
kind of CV
Relative Max
Relative Min
or Ledge |
 |
 Rel. Max Rel. Max
 Rel. Min Rel. Min
 Ledge Ledge |
 |
 Rel. Max Rel. Max
 Rel. Min Rel. Min
 Ledge Ledge |
 |
|
|
| [2] |
|
(Pg 261 #3, compare with [1] above) Let f(x) = |
1
3 |
x3 - 9x + 2 |
with domain of f restricted to: 0  x x  +2 +2 |
|
| |
|
(a)(2 pts) Enter BOTH CV's of f(x) into the
2nd row of the table below. Note: domain
endpoints are CV's. |
|
(b)(3 pts) Fill in the remaining empty boxes in the 3rd,
4th, and 5th rows of the table below. |
|
| |
|
|
 |
CV |
test value |
CV |
| x |
|
1 |
|
| f (x) |
|
|
|
| f '(x) |
 |
|
 |
kind
of
CV |
 Rel. Max. Rel. Max.
 Rel. Min. Rel. Min.
 Ledge Ledge |
 |
 Rel. Max. Rel. Max.
 Rel. Min. Rel. Min.
 Ledge Ledge |
|
 |
You
can
do
this
one |
|
|
| [3] |
|
(#31 Pg 288 one number changed) WalMart can buy American flags at $4 each, and
estimates that if they are sold for x dollars per flag (per day),
consumers will buy 20 - x flags. At what price
should WalMart sell its flags to maximize its (daily) profit P on those
flags. |
|
| |
(2 pts) For the problem in the box above, write an equation showing
the relationship between "x" and "P". |
| |
|
(Enter numbers in boxes) P(x) = |
|
x2 + |
|
x + |
|
; |
|
|
| |
(3 points) Differentiate the above P twice, find
any CVs of P, and name the x at which P
is largest. |
| |
|
P '(x) = |
|
; |
P "(x) = |
|
. Thus, P is biggest when x = |
|
|
| [4] |
(a)(1 pt)(Pg 309 #1a) Use a calculator to
express e2 as a decimal accurate to within 0.01 |
| |
(b)(2 pt)(Pg 325 part of #7) Without using a calculator, write e3 2 as an integer. 2 as an integer. |
| |
(c)(2 pts)(Pg 309 #21 one number changed) If 23-x = 8x, what is x? (show algebra work) |
| [5] |
|
(part of #11 Pg 355) Find f '(x) and f "(x) if f(x) = xex |
|
|
| [6] |
|
(more of #13 Pg 228) Find f "(x) if f(x) = |
1
3 |
x3 - 9x + 2 . |
|
|
(1 pt) Enter numbers in boxes : f "(x) = |
|
x2 + |
|
x + |
|
; |
|
|
|
Find the one candidate of f(x) above by filling in the table below.
A candidate is a value of x at which f "(x)
is either zero or undefined. ("IP" = "inflection point") |
|
|
|
| [7] |
(a)(#15 Pg 388)(1 pt) Find |
 |
( |
ex

2 |
+ |
x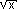 |
) |
dx |
|
| |
(b)(handout)(2 pts) Find |
 |
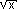


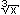 |
dx (The integrand is 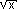 divided by divided by 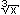 ) ) |
For the remaining 2 problems, if you use substitution, copy the left-hand
table (below) into your blue book, and fill in it's 4 empty boxes. If you use
integration by parts (IBP), copy the
right-hand table (below) into your blue book, and fill in it's 4 empty boxes.
Use no isolated differentials, i.e., do not write expressions like "du = 2xdx"
For substitution
|
u = |
|
|
y(u) = |
|
|
|
For IBP
|
u = |
u ' = |
|
v = |
v ' = |
|
| [8] |
(#17 Pg 403) Use substitution to find |
 |
(x + 1)( x2 + 2x + 5)12 dx |
|
 |
"time to
wake up" |
|
|
 2 as an integer.
2 as an integer.

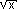

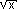


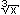
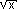 divided by
divided by 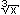 )
)
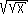 dx
dx